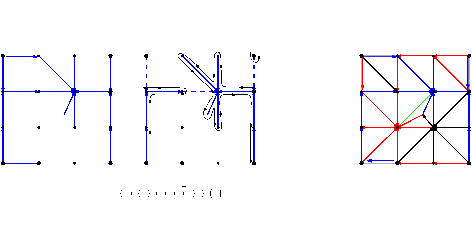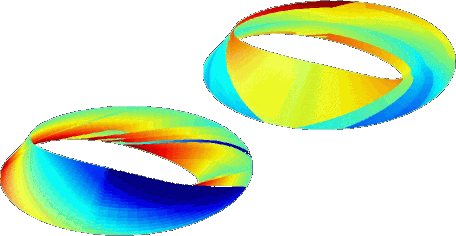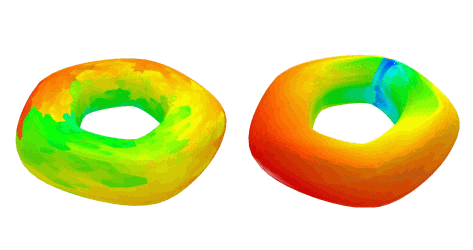Trabalho como Group Chief Data Officer na Ceva Santé Animale, depois de ter sido Lead Data Scientist no BCG Gamma, a entidade do Boston Consulting Group de AI for Business. Fui pesquisador e professor durante 15 anos no Departamento de Matemática da PUC do Rio de Janeiro. Trabalhava em diversas áreas da Matemática Aplicada: indo da Geometria e Topologia Computacionais à Computação Gráfica, da teoria de Morse discreta ao Processamento Geométrico, da Modelagem de Reservatórios à Dinâmica dos Fluidos Computacional.
Fui eleito membro afiliado da Academia Brasileira de Ciências para 2012/2016. Fui também convidado como keynote speaker no TopoInVis 2011 (apresentação, também disponível em pdf). Organizei junto com Esteban Clua o Sibgrapi 2009 na PUC e o ACM SoCG 2013 com Luis Peñaranda. Fui chair de programas junto com Ricardo Torres do Sibgrapi 2011. Sou editor das revistas Computer Graphics Forum, Image Processing On Line e Anais da Academia Brasileira de Ciências.
Participei, durante o meu pós-doutorado
do Grupo de Geometria Diferencial Discreta da Freie Universität Berlin, sobre a direção de Konrad Polthier,
do Grupo de Computação Gráfica da Universidade de Tel Aviv, sobre a direção de Daniel Cohen-Or,
e do Grupo de Geometria Discreta da Technische Universität Berlin, sobre a direção de Günter Ziegler.
Recebi um doutorado em Informática da Université Paris VI sobre a Compressão de Malhas a partir da Geometria, orientada pelo Professor Jean-Daniel Boissonnat do Projeto Géométrica (PRISME) do INRIA - Sophia Antipolis,
e um outro doutorado em Matemática da PUC - Rio de Janeiro, sobre os Complexos de Morse Discretos e Geométricos, orientado por Hélio Lopes, no Departamento de Matemática.
Lá também preparei o meu Mestrado em Matemática sobre a Construção de Funções de Morse Discretas, na PUC - Rio de Janeiro, que validou meu diploma da Telecom ParisTech, e assim o da École Polytechnique.
Publicações selecionadas
Passar o mouse sobre as imagens para acessar a publicação correspondente. Uma lista completa das minhas publicações está disponível aqui.
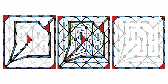
Discrete line fields on surfaces
(BibTeX)
Abstract: Vector fields and line fields, their counterparts without orientations on tangent lines, are familiar objects in the theory of dynamical systems. Among the techniques used in their study, the Morse–Smale decomposition of a (generic) field plays a fundamental role, relating the geometric structure of phase space to a combinatorial object consisting of critical points and separatrices. Such concepts led Forman to a satisfactory theory of discrete vector fields, in close analogy to the continuous case.
In this paper, we introduce discrete line fields. Again, our definition is rich enough to provide the counterparts of the basic results in the theory of continuous line fields: an Euler–Poincaré formula, a Morse–Smale decomposition and a topologically consistent cancellation of critical elements, which allows for topological simplification of the original discrete line field.
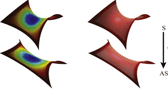
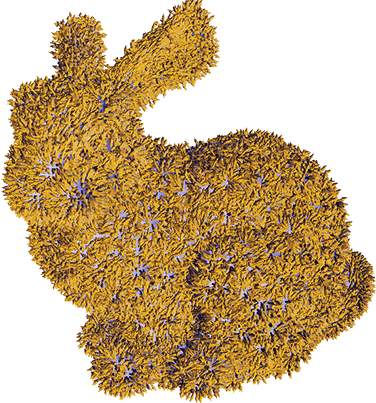
Estimating affine-invariant structures on triangle meshes
(BibTeX)
Abstract: Affine invariant measures are powerful tools to develop robust shape descriptors that can be applied, for example, to shape matching, shape retrieval, or symmetry detection problems. In this work we introduce estimators for the affine structure of surfaces represented by triangle meshes, i.e. affine co-normal and normal vectors, affine curvature tensors, affine mean and Gaussian curvatures, and affine principal directions and curvatures. The proposed method estimates the affine normal using a finite differences scheme together with a least-squares approximation, followed by a weighted average strategy to approach discrete affine curvature tensors. When compared to the exact geometric measures of analytic models, experiments on regular meshes obtain small error, which decreases for finer meshes, and outperforms the state-of-the-art method in some cases. Experiments to evaluate affine invariance show that the difference between measures before and after equi-affine transformations remains small even after large deformations.
Parameterized Complexity of Discrete Morse Theory
Abstract: Optimal Morse matchings reveal essential structures of cell complexes that lead to powerful tools to study discrete geometrical objects, in particular, discrete 3-manifolds. However, such matchings are known to be NP-hard to compute on 3-manifolds through a reduction to the erasability problem. Here, we refine the study of the complexity of problems related to discrete Morse theory in terms of parameterized complexity. On the one hand, we prove that the erasability problem is W[P]-complete on the natural parameter. On the other hand, we propose an algorithm for computing optimal Morse matchings on triangulations of 3-manifolds, which is fixed-parameter tractable in the treewidth of the bipartite graph representing the adjacency of the 1- and 2-simplices. This algorithm also shows fixed-parameter tractability for problems such as erasability and maximum alternating cycle-free matching. We further show that these results are also true when the treewidth of the dual graph of the triangulated 3-manifold is bounded. Finally, we discuss the topological significance of the chosen parameters and investigate the respective treewidths of simplicial and generalized triangulations of 3-manifolds.
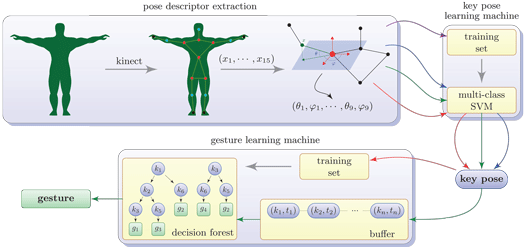
Simplified training for gesture recognition
Abstract: Since gesture is a fundamental form of human communication, its recognition by a computer generates a strong interest for many applications such as natural user interface and gaming. The popularization of real-time depth sensors brings such applications to the public at large. However, familiar gestures are culture-specific, and their automatic recognition must therefore result from a machine learning process. In particular this requires either teaching the user how to communicate with the machine, such as for popular mobile devices or gaming consoles, or tailoring the application to a specific public. The latter option serves a large number of applications such as sport monitoring, virtual reality or surveillance --- although it requires a usually tedious training.
This work intends to simplify the training required by gesture recognition methods. While the traditional procedure uses a set of key poses, which must be defined and trained, prior to a set of gestures that must also be defined and trained, we propose to automatically deduce the set of key poses from the gesture training. We represent a record of gestures as a curve in high dimension and robustly segment it according to the curvature of that curve. Then we use an asymmetric Hausdorff distance between gestures to define a discriminant key pose as the most distant pose between gestures. This further allows to dynamically group gestures by similarity. The training only requires the user to perform the gestures and eventually refine the gesture labeling. The generated set of key poses and gestures then fits in previous human action recognition algorithms. Furthermore, this semi-supervised learning allows re-using a previous training to extend the set of gestures the computer should be able to recognize.
Experimental results show that the automatically generated discriminant key poses lead to similar recognition accuracy as previous work.
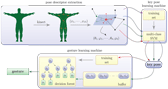
Online gesture recognition from pose kernel learning and decision forests
Pattern Recognition Letters 39: pp. 65-73 (april 2014)
Selected for publication from the Sibgrapi 2013 conference
Selected for publication from the Sibgrapi 2013 conference
(BibTeX)
Abstract: The recent popularization of real time depth sensors has diversified the potential applications of online gesture recognition to end-user natural user interface (NUI). This requires significant robustness of the gesture recognition to cope with the noisy data from the popular depth sensor, while the quality of the final NUI heavily depends on the recognition execution speed. This work introduces a method for real-time gesture recognition from a noisy skeleton stream, such as those extracted from Kinect depth sensors. Each pose is described using an angular representation of the skeleton joints. Those descriptors serve to identify key poses through a Support Vector Machine multi-class classifier, with a tailored pose kernel. The gesture is labeled on-the-fly from the key pose sequence with a decision forest, which naturally performs the gesture time control/warping and avoids the requirement for an initial or neutral pose. The proposed method runs in real time and its robustness is evaluated in several experiments.
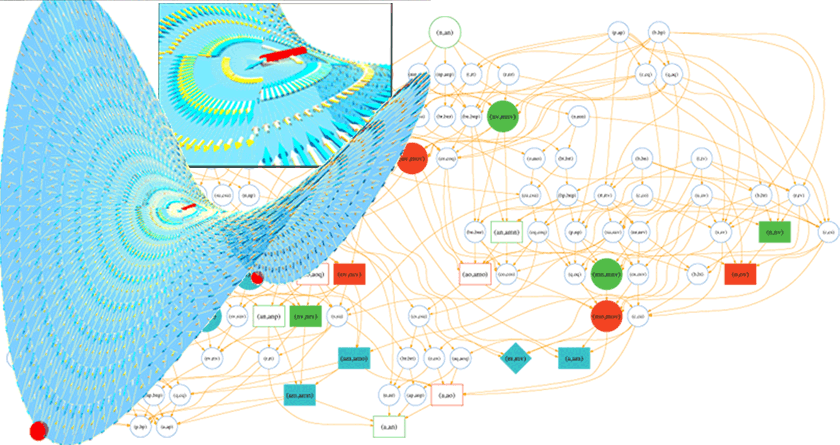
Streamline-based topological graph construction with application to self-animated images
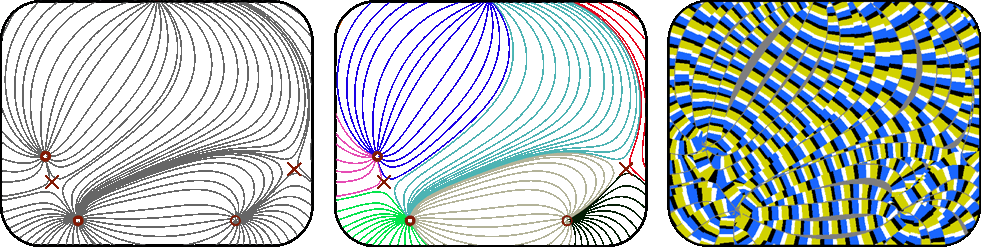
Abstract: Vector field analysis and visualization is a fundamental tool in science and engineering applications, raising the need for robust methods to capture and represent the global vector field behavior. One such representation, the topological graph, partitions the domain into regions where the flow of the vector field is homogeneous.
This work introduces a topological graph construction based on streamlines. It is guaranteed to produce a coherent result even when some singularities are not detected. This work also details an application of topological graphs to improve the generation of self-animated images. In this application, the streamline-based approach carries almost no overhead, since self-animated images already rely on streamlines, but leads to a threefold speed-up of the core processing..
This work introduces a topological graph construction based on streamlines. It is guaranteed to produce a coherent result even when some singularities are not detected. This work also details an application of topological graphs to improve the generation of self-animated images. In this application, the streamline-based approach carries almost no overhead, since self-animated images already rely on streamlines, but leads to a threefold speed-up of the core processing..
Parameterized Complexity of Discrete Morse Theory
Abstract: Optimal Morse matchings reveal essential structures of cell complexes which lead to powerful tools to study discrete geometrical objects, in particular discrete 3-manifolds. However, such matchings are known to be NP-hard to compute on 3-manifolds, through a reduction to the erasability problem.
Here, we refine the study of the complexity of problems related to discrete Morse theory in terms of parameterized complexity. On the one hand we prove that the erasability problem is W[P]-complete on the natural parameter. On the other hand we propose an algorithm for computing optimal Morse matchings on triangulations of 3-manifolds which is fixed-parameter tractable in the treewidth of the bipartite graph representing the adjacency of the 1- and 2-simplexes. This algorithm also shows fixed parameter tractability for problems such as erasability and maximum alternating cycle-free matching.
We further show that these results are also true when the treewidth of the dual graph of the triangulated 3-manifold is bounded. Finally, we investigate the respective treewidths of simplicial and generalized triangulations of 3-manifolds.
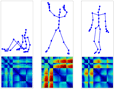
Distance matrices as invariant features for classifying MoCap data
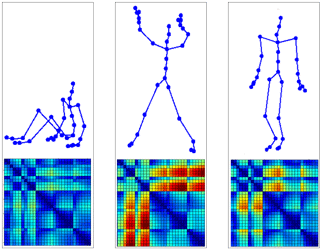
Abstract: This work introduces a new representation for Motion Capture data (MoCap) that is invariant under rigid transformation and robust for classification and annotation of MoCap data. This representation relies on distance matrices that fully characterize the class of identical postures up to the body position or orientation. This high dimensional feature descriptor is tailored using PCA and incorporated into an action graph based classification scheme. Classification experiments on publicly available data show the accuracy and robustness of the proposed MoCap representation.
Real-time gesture recognition from depth data through key poses learning and decision forests
Sibgrapi 2012 (XXV Conference on Graphics, Patterns and Images): pp. 268-275 (august 2012)
Selected for publication in Pattern Recognition Letters
Selected for publication in Pattern Recognition Letters
Abstract: Human gesture recognition is a challenging task with many applications. The popularization of real time depth sensors even diversifies potential applications to end-user natural user interface (NUI). The quality of such NUI highly depends on the robustness and execution speed of the gesture recognition. This work introduces a method for real-time gesture recognition from a noisy skeleton stream, such as the ones extracted from Kinect depth sensors. Each pose is described using a tailored angular representation of the skeleton joints. Those descriptors serve to identify key poses through a multi-class classifier derived from Support Vector learning machines. The gesture is labeled on-the-fly from the key pose sequence through a decision forest, that naturally performs the gesture time warping and avoids the requirement for an initial or neutral pose. The proposed method runs in real time and shows robustness in several experiments.
The Visual Computer - Special Issue on SIBGRAPI 2011
(BibTeX)
Abstract: This special issue of The Visual Computer contains expanded versions of eight papers presented at Sibgrapi 2011, the 24th Conference on Graphics, Patterns, and Images. Sibgrapi is the most traditional meeting in Latin America on Computer Graphics, Image Processing, Pattern Recognition and Computer Vision. In 2011, Sibgrapi was hosted in the beautiful city of Maceió, Alagoas, Brazil, being organized by the Instituto de Matemática of Universidade Federal de of Alagoas, and supported by Petrobras, CNPq, CAPES, FAPEAL, UFAL, SBM, and SBC.
Thanks to The Visual Computer’s editor in chief Nadia Magnenat-Thalmann, this issue presents eight papers selected from a pool of 46 papers presented during the technical sessions of the conference. They represent the main topics inside visual computing, from computational topology and modeling to rendering, visualization, and simulation.
Thanks to The Visual Computer’s editor in chief Nadia Magnenat-Thalmann, this issue presents eight papers selected from a pool of 46 papers presented during the technical sessions of the conference. They represent the main topics inside visual computing, from computational topology and modeling to rendering, visualization, and simulation.
Critical sets in discrete Morse theories: relating Forman and piecewise-linear approaches
Computer Aided Geometric Design 30(6): pp. 609-621 (july 2013)
Special issue on Foundations of Topological Analysis
Special issue on Foundations of Topological Analysis
Abstract: Morse theory inspired several robust and well grounded tools in discrete function analysis, geometric modeling and visualization. Such techniques need to adapt the original differential concepts of Morse theory in a discrete setting, generally using either piecewise--linear (PL) approximations or Forman's combinatorial formulation. The former carries the intuition behind Morse critical sets, while the latter avoids numerical integrations. Forman's gradients can be constructed from a scalar function using greedy strategies, although the relation with its PL gradient is not straightforward.
This work relates the critical sets of both approaches. It proves that the greedy construction on two-dimensional meshes actually builds an adjacent critical cell for each PL critical vertex. Moreover, the constructed gradient is globally aligned with the PL gradient. Those results allow adapting the many works in PL Morse theory for triangulated surfaces to Forman's combinatorial setting with low algorithmic complexity.
Affine-invariant curvature estimators for implicit surfaces
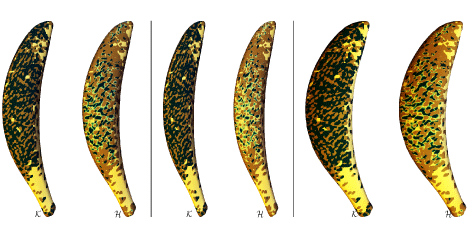
Abstract: Affine Differential Geometry provides a set of measures invariant under a larger set of transformations compared to rigid motions. This leads to several applications using robust shape descriptors. Although affine invariant operations are already used for surfaces, they do not intend to approximate the definitions of Affine Differential Geometry, which are the basis for further differential invariants. In this work we propose estimators for the local affine structure of an implicit surface, i.e. the affine metric, the co-normal and normal vectors, and the affine Gaussian and mean curvatures. The direct derivation of the formulae from the implicit function theorem lead to very intensive computations and numerical instabilities. This work further proposes a geometrical reduction allowing a much simpler and more stable formulae, and compares the results by incorporating the proposed estimators in Marching Cubes based algorithms.
Proceedings 24th Sibgrapi Conference on Graphics, Patterns and Images
Abstract: Sibgrapi 2011, the 24th Conference on Graphics, Patterns and Images was held in the marvelous city of Maceió, Alagoas, Brazil. To prepare this edition, we tried to revere the surrounding region of the Brazilian Nordeste by strongly involving researchers working in universities of that region in the organization of the different workshops of Sibgrapi 2011. Thanks to the dynamism of the general chairs, Professors Adelailson Peixoto, Dimas Martínez and Thales Vieira, we achieved a broad conference, opened from young students to international professionals through the several plenary talks, tutorials, workshops, festivals, and social activities. In particular, we had four very high quality plenary talks: Mathieu Desbrun (Caltech) on "Applied geometry for computer graphics and simulation"; James Wang (Penn State Unisversity) on "Automatic image tagging and aesthetic quality inferencing"; Alejandro C. Frery (UFAL) on "Information-theoric approaches for the analysis of speckled data"; and finally Claudio Silva (New York Univeristy) on "Measuring visualization correctness and effectiveness".
We also paid a lot of attention to the technical papers this year, significantly increasing the number of international committee members, improving the review process, and reforming the selection criteria to better cope with the diversity of areas of Sibgrapi. We received 123 submissions in the first phase, a significant increase compared to previous year. It should be mentioned that the overall quality of submissions was very good this year. During the double blind review process, we achieved motivating several discussions between the 176 referees and, after the disclosing of the reviews, with the authors. We discussed the acceptance of each paper with the reviewers and, for almost all papers, achieved a unanimous decision, leading to 46 technical papers accepted for presentation during the event.
The richness of the technical papers can be mainly credited to the authors, who have chosen Sibgrapi to submit their work, and to the reviewers, who dedicated a lot of their valuable time in the revision, discussion and final approval period. We also would like to thank the local organization committee, the several committees in charge of the different technical activities, the invited speakers, the session chairs, and the tutorial instructors. Finally, we are grateful to several institutions which were involved directly or indirectly in the organization of Sibgrapi 2011: Universidade Federal de Alagoas (UFAL), Pontifícia Universidade Católica do Rio de Janeiro (PUC-Rio), Universidade Estadual de Campinas (Unicamp), and the Brazilian Computer Society (SBC).
We also paid a lot of attention to the technical papers this year, significantly increasing the number of international committee members, improving the review process, and reforming the selection criteria to better cope with the diversity of areas of Sibgrapi. We received 123 submissions in the first phase, a significant increase compared to previous year. It should be mentioned that the overall quality of submissions was very good this year. During the double blind review process, we achieved motivating several discussions between the 176 referees and, after the disclosing of the reviews, with the authors. We discussed the acceptance of each paper with the reviewers and, for almost all papers, achieved a unanimous decision, leading to 46 technical papers accepted for presentation during the event.
The richness of the technical papers can be mainly credited to the authors, who have chosen Sibgrapi to submit their work, and to the reviewers, who dedicated a lot of their valuable time in the revision, discussion and final approval period. We also would like to thank the local organization committee, the several committees in charge of the different technical activities, the invited speakers, the session chairs, and the tutorial instructors. Finally, we are grateful to several institutions which were involved directly or indirectly in the organization of Sibgrapi 2011: Universidade Federal de Alagoas (UFAL), Pontifícia Universidade Católica do Rio de Janeiro (PUC-Rio), Universidade Estadual de Campinas (Unicamp), and the Brazilian Computer Society (SBC).
Stereo music visualization through manifold harmonics
The Visual Computer 27(10): pp. 905-916 (october 2011)
Selected for publication from the Sibgrapi 2010 conference
Selected for publication from the Sibgrapi 2010 conference
Abstract: Music visualizations are nowadays included with virtually any media player.
They usually rely on harmonic analysis of each sound channel, which automatically generate parameters for procedural image generation.
However, only few music visualizations make use of 3d shapes. This paper proposes to use spectral mesh processing techniques, here manifold harmonics, to produce 3d stereo music visualization.
The images are generated from 3d models by deforming an initial shape, mapping the sound frequencies to the mesh harmonics.
A symmetry criterion is introduced to enhance the stereo effects on the deformed shape.
A concise representation of the frequency mapping is proposed to allow for an animated gallery interface with genetic reproduction. Such galleries let the user quickly navigate between visual effects.
Rendering such animated galleries in real-time is a challenging task, since it requires computing and rendering the deformed shapes at a very high rate. This paper introduces a direct GPU implementation of manifold harmonics filters, which allows the displaying of the animated galleries.
Geometric invariant calculus and estimation: an introduction to Euclidean and affine geometries
Abstract: Book published in the context of the 28th Brazilian Mathematical Colloquium.
Interactive 3D caricature from harmonic exaggeration
Abstract: A common variant of caricature relies on exaggerating characteristics of a shape that differs from a reference template, usually the distinctive traits of a human portrait.
This work introduces a caricature tool that interactively emphasizes the differences between two three-dimensional meshes. They are represented in the manifold harmonic basis of the shape to be caricatured, providing intrinsic controls on the deformation and its scales. It further provides a smooth localization scheme for the deformation. This lets the user edit the caricature part by part, combining different settings and models of exaggeration, all expressed in terms of harmonic filter. This formulation also allows for interactivity, rendering the resulting 3d shape in real time.
Implicit curves and surfaces: elements of differential and discrete geometries
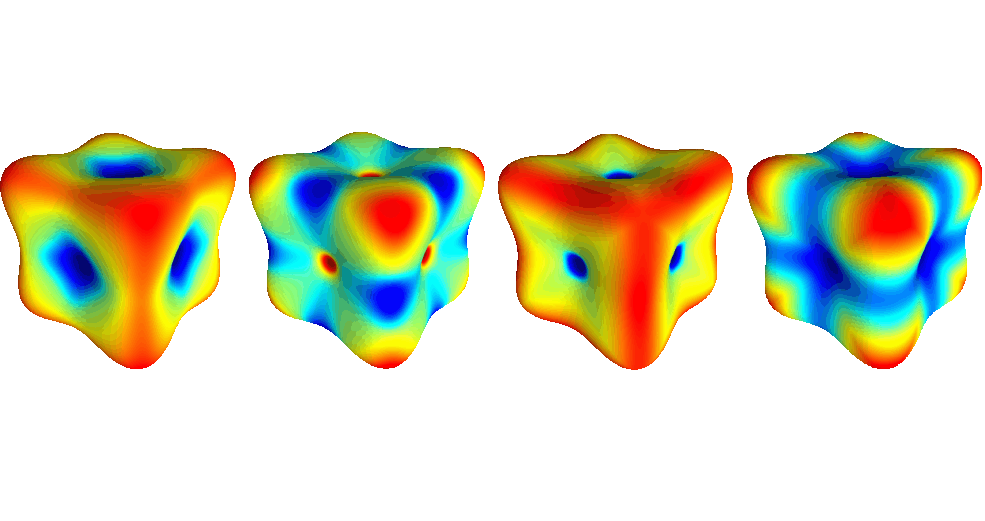
Abstract: Book published in the context of the 1st Mathematical Colloquium of the North-East Region.
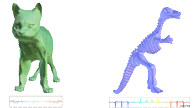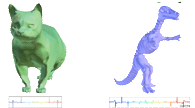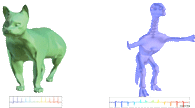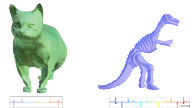
Fast generation of pointerless octree duals
Abstract: Geometry processing applications frequently rely on octree structures, since they provide simple and efficient hierarchies for discrete data. However, octrees do not guarantee direct continuous interpolation of this data inside its nodes. This motivates the use of the octree's dual structure, which is one of the simplest continuous hierarchical structures. With the emergence of pointerless representations, with their ability to reduce memory footprint and adapt to parallel architectures, the generation of duals of pointerless octrees becomes a natural challenge. This work proposes strategies for dual generation of static or dynamic pointerless octrees. Experimentally, those methods enjoy the memory reduction of pointerless representations and speed up the execution by several factors compared to the usual recursive generation.
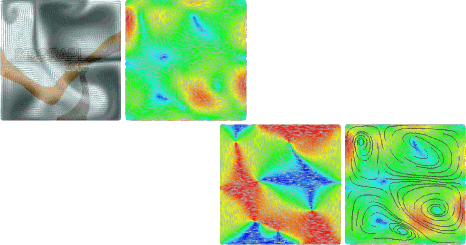
Topology aware vector field denoising
Abstract: Recent developments in data acquisition technology enable to directly capture real vector fields, helping for a better understanding of physical phenomena. However measured data is corrupted by noise, puzzling the understanding of the phenomena. This turns the task of removing noise, i.e. denoising, an essential preprocessing step for a better analysis of the data. Nonetheless a careful use of denoising is required since usual algorithms not only remove the noise but can also eliminate information, in particular the vector field singularities, which are fundamental features in the analysis. This paper proposes a semi-automatic vector field denoising methodology, where the user visually controls the topological changes caused by classical vector field filtering in scale-spaces.
Tuning manifold harmonics filters
Sibgrapi 2010 (XXIII Conference on Graphics, Patterns and Images): pp. 110-117 (august 2010)
Selected for publication in The Visual Computer
Selected for publication in The Visual Computer
Abstract: There are several techniques for automatic music visualization, which are included with virtually any media player. The basic ingredient of those techniques is spectral analysis of the sound, used to automatically generate parameters for procedural image generation. However, only a few music visualizations rely on 3d models. This paper proposes to use spectral mesh processing techniques, namely manifold harmonics, to produce 3d music visualization. The images are generated from 3d models by deforming an initial shape, mapping the sound frequencies to the mesh harmonics. A concise representation of such frequency mapping is proposed to permit for an animated gallery interface with genetic reproduction. Such galleries allow the user to quickly navigate between visual effects. Rendering such animated galleries in real-time is a challenging task, since it requires computing and rendering the deformed shapes at a very high rate. This paper introduces a direct GPU implementation of manifold harmonics filters, which allows to display animated gallery.
Role of arches in the generation of shear bands in a dense 3D granular system under shear
Latin American Workshop on Nonlinear Phenomena (Journal of Physics: Conference Series 246(1)): pp. 2016 (september 2010)
Abstract: A model for propagation of arches on cubic lattices, to simulate the internal mobility of grains in a dense granular system under shear is proposed. In this model, the role of the arches in granular transportation presents a non-linear dependence on the local values of the stress components that can be modeled geometrically. In particular, we study a modified Couette flow and were able to reproduce qualitatively the experimental results found in the literature.
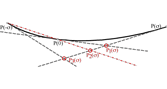
Projective splines and estimators for planar curves
Journal of Mathematical Imaging and Vision 36(1): pp. 81-89 (january 2010)
Extended version of the Sibgrapi 2008 conference .
Extended version of the Sibgrapi 2008 conference .
Abstract: Recognizing shapes in multiview imaging is still a challenging task, which usually relies on geometrical invariants estimations. However, very few geometric estimators that achieve projective invariance have been devised. This paper proposes a projective length and a projective curvature estimators for plane curves, when the curves are represented by points together with their tangent directions. In this context, the estimations can be performed with only three point-tangent samples for the projective length and five samples for the projective curvature. The proposed length and curvature estimator are based on projective splines built by fitting logarithmic spirals to the point-tangent samples. They are projective invariant and convergent.
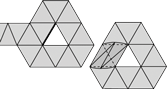
Topological mesh operators
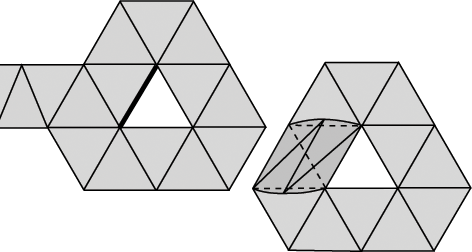
Abstract: In this paper we introduce an unified framework for topological manipulation on triangulated 2-manifolds with or without boundary. We show that there are two kinds of primitive operators on the underlying meshes: operators that change the topological characteristic of the mesh and operators that just modify its combinatorial structure. We present such operators and demonstrate that they provide a complete and coherent set of elementary operations for mesh construction and editing.
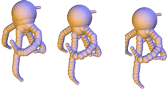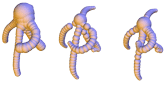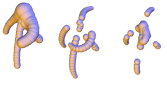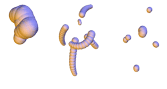
Scale-space for union of 3d balls
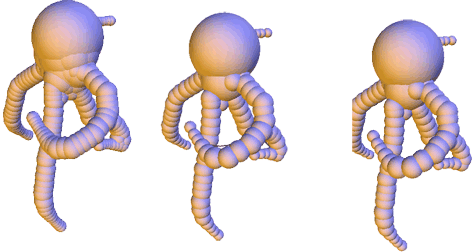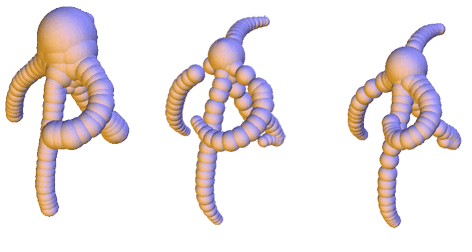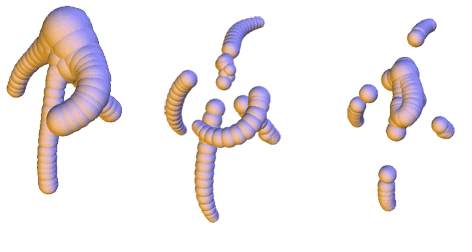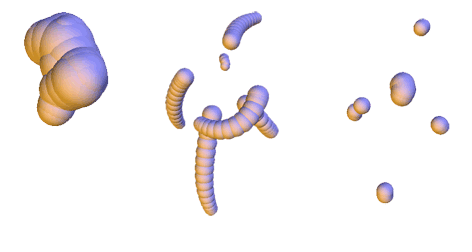
Sibgrapi 2009 (XXII Brazilian Symposium on Computer Graphics and Image Processing): pp. 9-16 (october 2009)
Abstract: Shape discretization through union of weighted points or balls appears as a common representation in different fields of computer graphics and geometric modeling. Among others, it has been very successful for implicit surface reconstruction with radial basis functions, molecular atomic models, fluid simulation from particle systems and deformation tracking with particle filters. These representations are commonly generated from real measurements or numerical computations, which may require filtering and smoothing operations. This work proposes a smoothing mechanism for union of balls that tries to inherit from the scale-space properties of bi-dimensional curvature motion: it avoids disconnecting the shape, prevents self-intersection, regularly decreases the area and convexifies the shape. The smoothing is computed iteratively by moving each ball of the union according to a combination of projected planar curvature motions. Experiments exhibits nice properties of this scale-space.
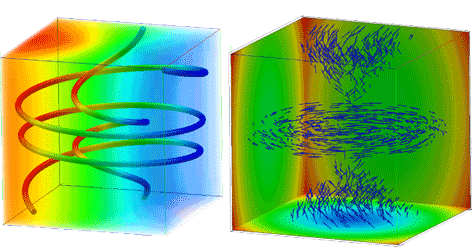
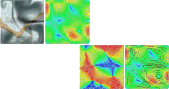
Random walks for vector field denoising
Sibgrapi 2009 (XXII Brazilian Symposium on Computer Graphics and Image Processing): pp. 112-119 (october 2009)
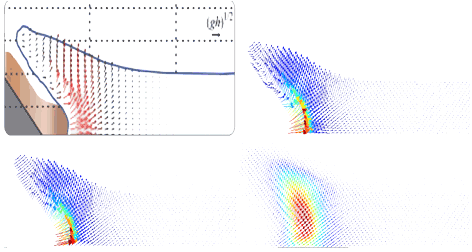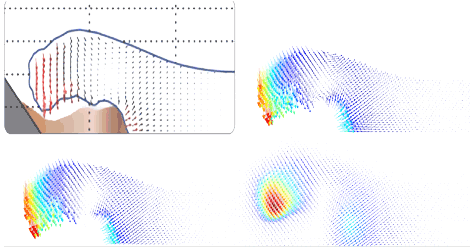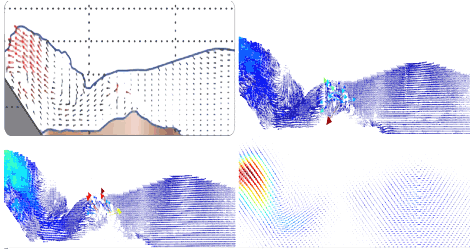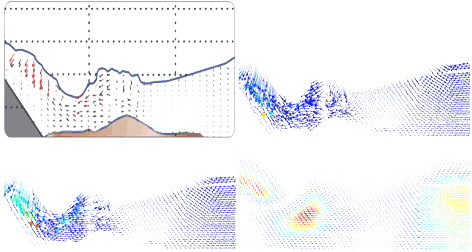
Abstract: In recent years, several devices allow to directly measure real vector fields, leading to a better understanding of fundamental phenomena such as fluid simulation or brain water movement. This turns vector field visualization and analysis important tools for many applications in engineering and in medicine. However, real data is generally corrupted by noise, puzzling the understanding provided by those tools. Those tools thus need a denoising step as preprocessing, although usual denoising removes discontinuities, which are fundamental for vector field analysis. This paper proposes a novel method for vector field denoising based on random walks which preserve those discontinuities. It works in a meshless setting; it is fast, simple to implement, and shows a better performance than the traditional gaussian denoising technique.
Geometry super-resolution by example
Sibgrapi 2009 (XXII Brazilian Symposium on Computer Graphics and Image Processing): pp. 40-47 (october 2009)
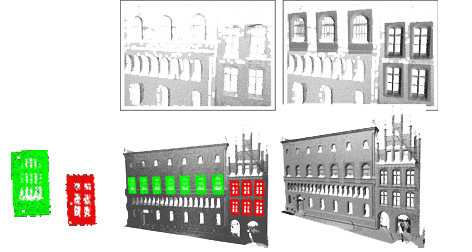
Abstract: The acquisition of high-resolution 3D models still requires delicate and time-consuming processes. In particular, each detail of the object should be scanned separately, although they may be similar. This can be simplified by copying a small set of details at different places of the model, synthesizing high geometric resolution from details exemplars, as introduced in this paper for three different contexts : when the detail exemplars are scanned separately at high resolution, when they are synthesized or edited from other models, or when they are obtained by accumulating repeated instances of the detail in the low-resolution scan. The main challenge here is to correctly register the high-resolution details with the low resolution model. To address this issue, this work proposes a careful resolution manipulation of 3D scans at each step of an automatic registration pipeline, combined with a robust selection of alignments. This results in a fully automatic process for geometry super-resolution by example. Experiments on synthetic and real data sets show applicability in different contexts, including resolution increase, noise removal by example and geometric texture insertion.
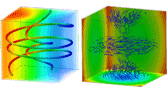
Support vectors learning for vector field reconstruction
Sibgrapi 2009 (XXII Brazilian Symposium on Computer Graphics and Image Processing): pp. 104-111 (october 2009)
Abstract: Sampled vector fields generally appear as measurements of real phenomena. They can be obtained by the use of a Particle Image Velocimetry acquisition device, or as the result of a physical simulation, such as a fluid flow simulation, among many examples. This paper proposes to formulate the unstructured vector field reconstruction and approximation through Machine-Learning. The machine learns from the samples a global vector field estimation function that could be evaluated at arbitrary points from the whole domain. Using an adaptation of the Support Vector Regression method for multi-scale analysis, the proposed method provides a global, analytical expression for the reconstructed vector field through an efficient non-linear optimization. Experiments on artificial and real data show a statistically robust behavior of the proposed technique.
Discrete affine minimal surfaces with indefinite metric
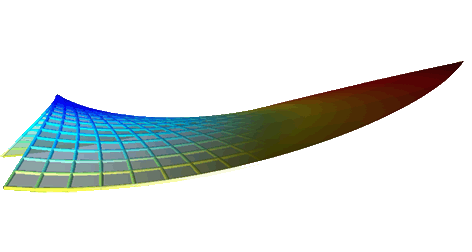
Abstract: Inspired by the Weierstrass representation of smooth affine minimal surfaces with indefinite metric, we propose a constructive process producing a large class of discrete surfaces that we call discrete affine minimal surfaces. We show that they are critical points of an affine area functional defined on the space of quadrangular discrete surfaces. The construction makes use of asymptotic coordinates and allows defining the discrete analogs of some differential geometric objects, such as the normal and co normal vector fields, the cubic form and the compatibility equations.
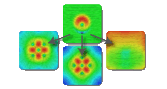
Meshless Helmholtz-Hodge decomposition
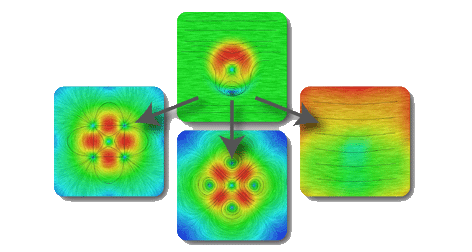
Abstract: Vector fields analysis traditionally distinguishes conservative (curl-free) from mass preserving (divergence-free) components. The Helmholtz-Hodge decomposition allows separating any vector field into the sum of three uniquely defined components: curl-free, divergence-free and harmonic. This decomposition is usually achieved by using mesh-based methods such as finite differences or finite elements. This work presents a new meshless approach to the Helmholtz-Hodge decomposition for the analysis of 2D discrete vector fields. It embeds into the SPH particle-based framework. The proposed method is efficient and can be applied to extract features from a 2D discrete vector field and to multiphase fluid flow simulation to ensure incompressibility.
Meshless fluid simulation: introduction to SPH methods
Abstract: Book published in the context of the 27th Brazilian Mathematical Colloquium.
Particle-based viscoplastic fluid/solid simulation
Abstract: Simulations of viscoplastic materials are traditionally governed by continuum mechanics. The viscous behavior is typically modeled as an internal force, defined by diverse quantities. This work introduces a fluid model to simulate the viscoplastic effect of solid materials, such as plastic, wax, clay and polymer. Our method consists in modeling a solid object through a non-Newtonian fluid with high viscosity. This fluid~simulation uses the Smoothed Particle Hydrodynamics method and the viscosity is formulated by using the General Newtonian Fluid model. This model concentrates the viscoplasticity in a single parameter. Our results show clear effects of creep, melting, hardening and flowing.
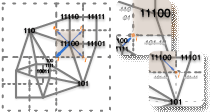
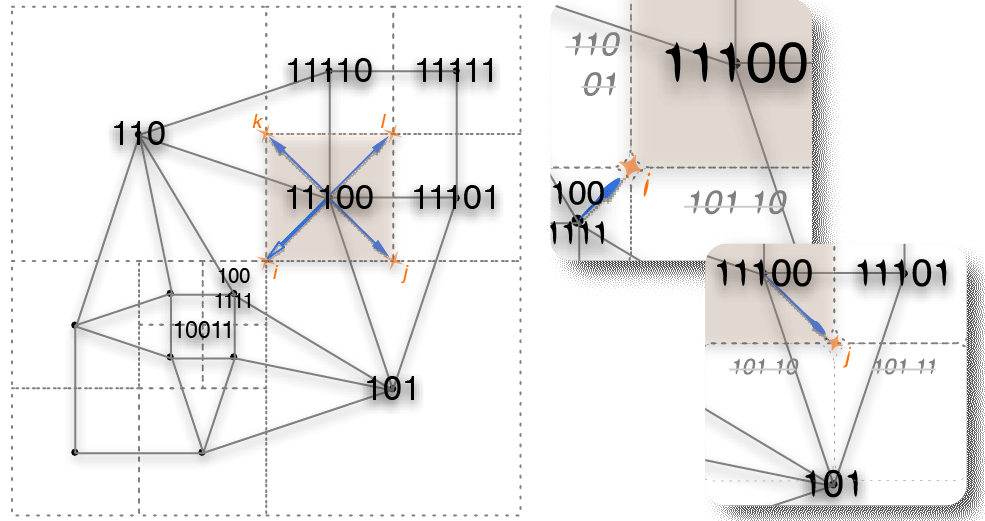
Schnyder woods for higher genus triangulated surfaces, with applications to encoding
Discrete and Computational Geometry 42(3): pp. 489-516 (october 2009)
Selected for publication from the SoCG 2008 conference
Selected for publication from the SoCG 2008 conference
Abstract: Schnyder woods are a well-known combinatorial structure for plane triangulations, which yields a decomposition into 3 spanning trees. We extend here definitions and algorithms for Schnyder woods to closed orientable surfaces of arbitrary genus. In particular, we describe a method to traverse a triangulation of genus g and compute a so-called g-Schnyder wood on the way. As an application, we give a procedure to encode a triangulation of genus g and n vertices in 4n+O(g log(n)) bits. This matches the worst-case encoding rate of Edgebreaker in positive genus. All the algorithms presented here have execution time O((n+g)g), hence are linear when the genus is fixed.
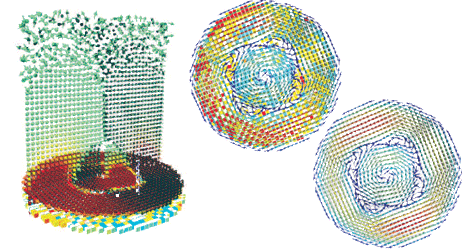
Arch generated shear bands in granular systems
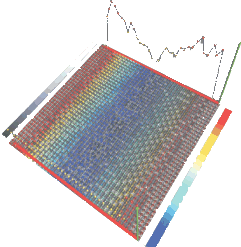
Abstract: We propose an arch based model, on cubic and square lattices, to simulate the internal mobility of grains, in a dense granular system under shear. In this model, the role of the arches in granular transport presents a non-linear dependence on the local values of the stress components that can be modeled geometrically. This non-linearity is very important since a linear dependence on the stress will make the models behave similarly to viscous fluids, which will not reproduce highly interesting properties of the sheared systems such as shear bands. In particular, we study a modified Couette flow and find the appearance of shear bands in accordance with the literature.
Learning good views through intelligent galleries
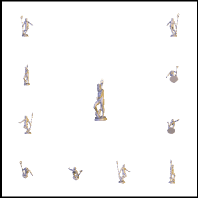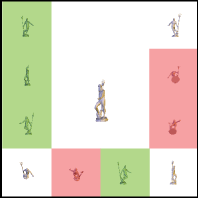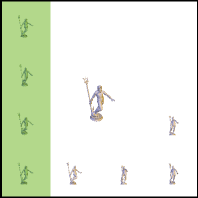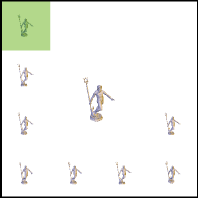
Abstract: The definition of a good view of a 3D scene is highly subjective and strongly depends on both the scene content and the 3D application. Usually, camera placement is performed directly by the user, and that task may be laborious. Existing automatic virtual cameras guide the user by optimizing a single rule, e.g. maximizing the visible silhouette or the projected area. However, the use of a static pre-defined rule may fail in respecting the user s subjective understanding of the scene. This work introduces intelligent design galleries, a learning approach for subjective problems such as the camera placement. The interaction of the user with a design gallery teaches a statistical learning machine. The trained machine can then imitate the user, either by pre-selecting good views or by automatically placing the camera. The learning process relies on a Support Vector Machines for classifying views from a collection of descriptors, ranging from 2D image quality to 3D features visibility. Experiments of the automatic camera placement demonstrate that the proposed technique is efficient and handles scenes with occlusion and high depth complexities. This work also includes user validations of the intelligent gallery interface.
Symmetry-based completion
GRAPP 2009 (Fourth International Conference on Computer Graphics Theory and Applications)(february 2009)
Abstract: Acquired images often present missing, degraded or occluded parts. Inpainting techniques try to infer lacking information, usually from valid information nearby. This work introduces a new method to complete missing parts from an image using structural information of the image. Since natural and human-made objects present several symmetries, the image structure is described in terms of axial symmetries, and extrapolating the symmetries of the valid parts completes the missing ones. In particular, this allows inferring both the edges and the textures. This research started as a project for the course Reconstruction Methods at IMPA in fall 2007.
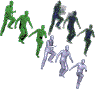
Space-time surface reconstruction using incompressible flow
Abstract: We introduce a volumetric space-time technique for the reconstruction of moving and deforming objects from point data. The output of our method is a four-dimensional space-time solid, made up of spatial slices, each of which is a three-dimensional solid bounded by a watertight manifold. The motion of the object is described as an incompressible flow of material through time. We optimize the flow so that the distance material moves from one time frame to the next is bounded, the density of material remains constant, and the object remains compact. This formulation overcomes deficiencies in the acquired data, such as persistent occlusions, errors, and missing frames. We demonstrate the performance of our flow-based technique by reconstructing coherent sequences of watertight models from incomplete scanner data.
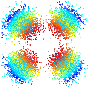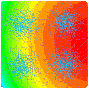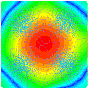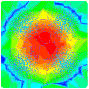
Approximations by smooth transitions in binary space partitions
Sibgrapi 2008 (XXI Brazilian Symposium on Computer Graphics and Image Processing): pp. 230-236 (october 2008)
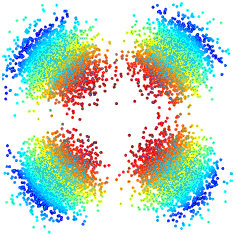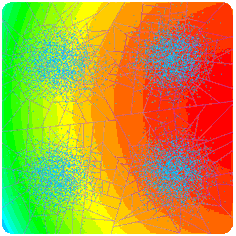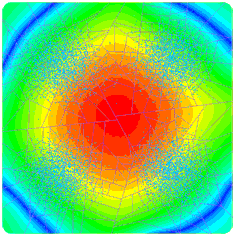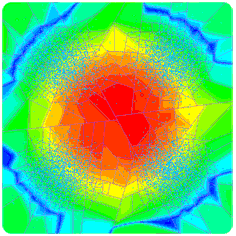
Abstract: This work proposes a simple approximation scheme for discrete data that leads to an infinitely smooth result without global optimization. It combines the flexibility of Binary Space Partitions Trees with the statistical robustness of Smooth Transition Regression Trees. The construction of the tree is straightforward and easily controllable, using error-driven metrics or external constraints. Moreover, it leads to a concise representation. Applications on synthetic and real data, both scalar and vector-valued demonstrated the effectiveness of this approach.
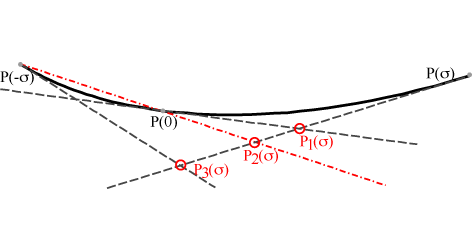
Projective estimators for point-tangent representations of planar curves
Sibgrapi 2008 (XXI Brazilian Symposium on Computer Graphics and Image Processing): pp. 223-229 (october 2008)
Extended in Journal of Mathematical Imaging and Vision.
Extended in Journal of Mathematical Imaging and Vision.
Abstract: Recognizing shapes in multiview imaging is still a challenging task, which usually relies on geometrical invariants estimations. However, very few geometric estimators that are projective invariant have been devised. This paper proposes projective length and projective curvature estimators for plane curves, when the curves are represented by points together with their tangent directions. In this context, the estimations can be performed with only the four point-tangent samples for the projective length and five for the projective curvature. The proposed length estimator is based on affine estimators and is proved to be convergent. The curvature estimator relies on the length to fit logarithmic spirals to the point-tangent samples. It is projective invariant and experiments indicate its convergence. Preliminary results using both estimators together are promising, although the estimators lack of robustness would require additional work for noisy cases.
Schnyder woods for higher genus triangulated surfaces
SoCG 2008 (XXIV ACM Symposium on Computational Geometry): pp. 311-319 (june 2008)
Selected for publication in Discrete and Computational Geometry
Selected for publication in Discrete and Computational Geometry
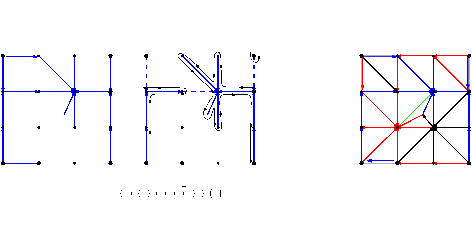
Abstract: We study a well-known characterization of planar graphs, also called Schnyder wood or Schnyder labeling, which yields a decomposition into vertex spanning trees. The goal is to extend previous algorithms and characterizations designed for planar graphs (corresponding to combinatorial surfaces with the topology of the sphere, i.e., of genus 0) to the more general case of graphs embedded on surfaces of arbitrary genus. First, we define a new traversal order of the vertices of a triangulated surface of genus g together with an orientation and coloration of the edges that extends the one proposed by Schnyder for the planar case. As a by-product we show how some recent schemes for compression and compact encoding of graphs can be extended to the higher genus case. All the algorithms presented here have linear time complexity.
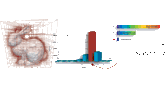
Statistical optimization of octree searches
Abstract: This work emerged from the following observation: usual search procedures for octrees start from the root to retrieve the data stored at the leaves. But since the leaves are the farthest nodes to the root, why start from the root? With usual octree representations, there is no other way to access a leaf. However, hashed octrees allow direct access to any node, given its position in space and its depth in the octree. Search procedures take the position as an input, but the depth remains unknown. This work proposes to estimate the depth of an arbitrary node through a statistical optimization of the average cost of search procedures. Since the highest costs of these algorithms are obtained when starting from the root, this method improves on both the memory footprint by the use of hashed octrees, and execution time through the proposed optimization.
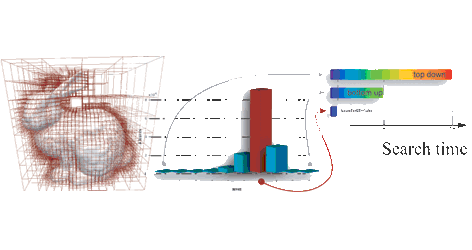
An iterative framework for registration with reconstruction
Vision, Modeling, and Visualization 2007 : pp. 101-108 (november 2007)
Abstract: The core of most registration algorithms aligns scan data by pairs, minimizing their relative distance. This local optimization must generally pass through a validation procedure to ensure the global coherence of the resulting alignments. This work introduces an iterative framework to guarantee the global coherence of the registration process. The iteration alternates registration and reconstruction steps, including alignments with the proper reconstructed surface, until the alignment of all the scans converges. The framework adapts to different contexts by choosing which scans are aligned and which are used for the reconstruction. This choice is based on the alignment and reconstruction errors. Derivations of this framework are presented with a rough automatic registration, increasing its robustness.
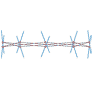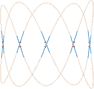
Combining points and tangents into parabolic polygons: an affine invariant model for plane curves
Journal of Mathematical Imaging and Vision 29(2-3): pp. 131-140 (november 2007)
Selected for publication from the Sibgrapi 2006 conference Check also the technical report Convergence of affine estimators on parabolic polygons.
Selected for publication from the Sibgrapi 2006 conference Check also the technical report Convergence of affine estimators on parabolic polygons.
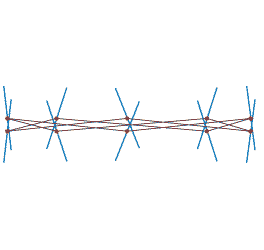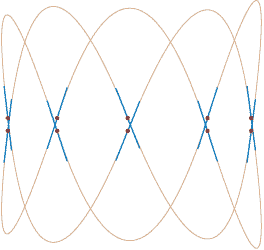
Abstract: Image and geometry processing applications estimate the local geometry of objects using information localized at points. They usually consider information about the tangents as a side product of the points coordinates. This work proposes parabolic polygons as a model for discrete curves, which intrinsically combines points and tangents. This model is naturally affine invariant, which makes it particularly adapted to computer vision applications. As a direct application of this affine invariance, this paper introduces an affine curvature estimator that has a great potential to improve computer vision tasks such as matching and registering. As a proof-of-concept, this work also proposes an affine invariant curve reconstruction from point and tangent data.
Interactive topology-aware surface reconstruction
Abstract: The reconstruction of a complete watertight model from scan data is still a difficult process. In particular, since scanned data is often incomplete, the reconstruction of the expected shape is an ill-posed problem. Techniques that reconstruct poorly-sampled areas without any user intervention fail in many cases to faithfully reconstruct the topology of the model. The method that we introduce in this paper is topology-aware: it uses minimal user input to make correct decisions at regions where the topology of the model cannot be automatically induced with a reasonable degree of confidence. We first construct a continuous function over a three-dimensional domain. This function is constructed by minimizing a penalty function combining the data points, user constraints, and a regularization term. The optimization problem is formulated in a mesh-independent manner, and mapped onto a specific mesh using the finite-element method. The zero level-set of this function is a first approximation of the reconstructed surface. At complex under-sampled regions, the constraints might be insufficient. Hence, we analyze the local topological stability of the zero level-set to detect weak regions of the surface. These regions are suggested to the user for adding local inside/outside constraints by merely scribbling over a 2D tablet. Each new user constraint modifies the minimization problem, which is solved incrementally. The process is repeated, converging to a topology-stable reconstruction. Reconstructions of models acquired by a structured-light scanner with a small number of scribbles demonstrate the effectiveness of the method.
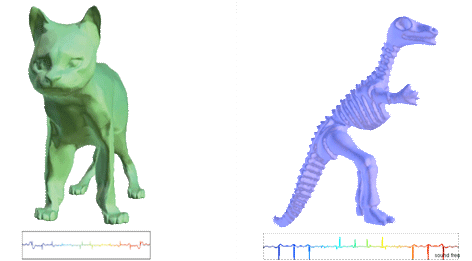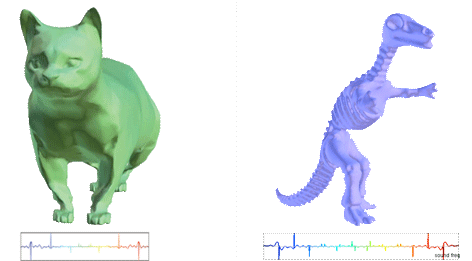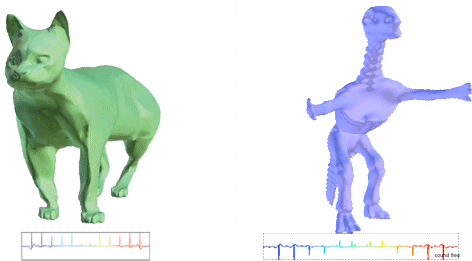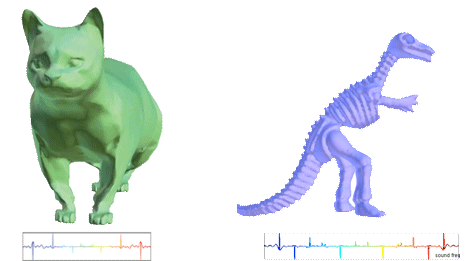
On-the-fly curve-skeleton computation for 3d shapes
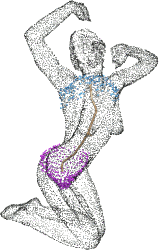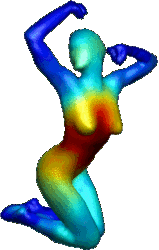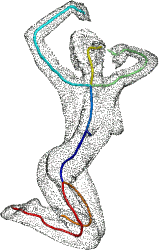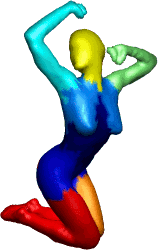
Abstract: The curve-skeleton of a 3D object is an abstract geometrical and topological representation of its 3D shape. It maps the spatial relation of geometrically meaningful parts to a graph structure. Each arc of this graph represents a part of the object with roughly constant diameter or thickness, and approximates its centerline. This makes the curve-skeleton suitable to describe and handle articulated objects such as characters for animation. We present an algorithm to extract such a skeleton on-the-fly, both from point clouds and polygonal meshes. The algorithm is based on a deformable model evolution that captures the object s volumetric shape. The deformable model involves multiple competing fronts, which evolve inside the object in a coarse-to-fine manner. We first track these fronts centers, and then merge and filter the resulting arcs to obtain a curve-skeleton of the object. The process inherits the robustness of the reconstruction technique, being able to cope with noisy input, intricate geometry and complex topology. It creates a natural segmentation of the object and computes a center curve for each segment while maintaining a full correspondence between the skeleton and the boundary of the object.
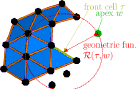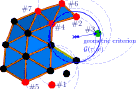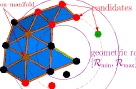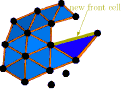
GEncode: geometry-driven compression for general meshes
Computer Graphics Forum 25(4): pp. 685-695 (december 2006)
Selected for publication from the Sibgrapi 2005 conference
Selected for publication from the Sibgrapi 2005 conference
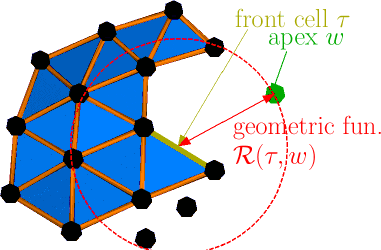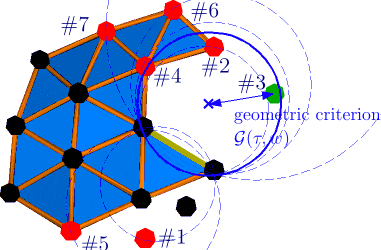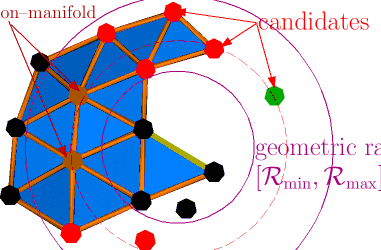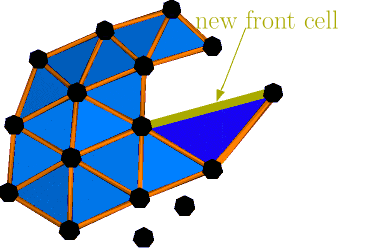
Abstract: Performances of actual mesh compression algorithms vary significantly depending on the type of model it encodes. These methods rely on prior assumptions on the mesh to be efficient, such as regular connectivity, simple topology and similarity between its elements. However, these priors are implicit in usual schemes, harming their suitability for specific models. In particular, connectivity-driven schemes are difficult to generalize to higher dimensions and to handle topological singularities. GEncode is a new single-rate, geometry-driven compression scheme where prior knowledge of the mesh is plugged into the coder in an explicit manner. It encodes meshes of arbitrary dimension without topological restrictions, but can incorporate topological properties, such as manifoldness, to improve the compression ratio. Prior knowledge of the geometry is taken as an input of the algorithm, represented by a function of the local geometry. This suits particularly well for scanned and remeshed models, where exact geometric priors are available. Compression results surfaces and volumes are competitive with existing schemes.
Particle-based non-Newtonian fluid animation for melting objects
Sibgrapi 2006 (XIX Brazilian Symposium on Computer Graphics and Image Processing): pp. 78-85 (october 2006)
Extended in Computer-Aided Design.
Extended in Computer-Aided Design.
Abstract: This paper presents a new visually realistic animation technique for objects that melt and flow. It simulates viscoplastic properties of materials such as metal, plastic, wax, polymer and lava. The technique consists in modeling the object by the transition of a non-Newtonian fluid with high viscosity to a liquid of low viscosity. During the melting, the viscosity is formulated using the General Newtonian fluids model, whose properties depend on the local temperature. The phase transition is then driven by the heat equation. The fluid simulation framework uses a variation of the Lagrangian method called Smoothed Particle Hydrodynamics. This paper also includes several schemes that improve the efficiency and the numerical stability of the equations.
Robust adaptive meshes for implicit surfaces
Sibgrapi 2006 (XIX Brazilian Symposium on Computer Graphics and Image Processing): pp. 205-212 (october 2006)
Abstract: This work introduces a robust algorithm for computing good polygonal approximations of implicit surfaces, where robustness entails recovering the exact topology of the implicit surface. Furthermore, the approximate triangle mesh adapts to the geometry and to the topology of the real implicit surface. This method generates an octree subdivided according to the interval evaluation of the implicit function in order to guarantee the robustness, and to the interval automatic differentiation in order to adapt the octree to the geometry of the implicit surface. The triangle mesh is then generated from that octree through an enhanced dual marching.
Point set compression through BSP quantization
Sibgrapi 2006 (XIX Brazilian Symposium on Computer Graphics and Image Processing): pp. 229-236 (october 2006)
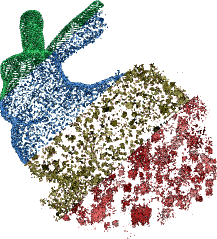
Abstract: This work introduces a new compression scheme for point sets. This scheme relies on an adaptive binary space partition (BSP) that takes into account the geometric structure of the point set. This choice introduces geometrical rather than combinatorial information in the compression scheme. In order to effectively improve the final compression ratio, this partition is encoded in a progressive manner, decreasing the number of bits used for the quantization at each subdivision. This strategy distributes the extra cost of the geometry encoding onto the maximal number of points, compressing in average 15% more than previous techniques.
Exploratory visualization based on multidimensional transfer functions and star coordinates
Sibgrapi 2006 (XIX Brazilian Symposium on Computer Graphics and Image Processing): pp. 273-280 (october 2006)
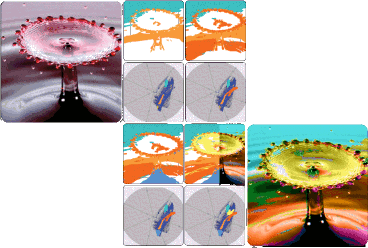
Abstract: Exploration and analysis of multivariate data play an important role in different domains. This work proposes a simple interface prototype that allows a human user to visually explore multivariate spatial objects, such as images, sequence of images or volume. It uses star coordinates as a widget to display the multivariate data on the computer 2D screen. The user then identifies a feature on this powerful coordinate system by mapping a selected feature region on that widget to a color and opacity. As a visual result, the feature is rendered on the objects space composing this map and the star coordinates projection. Some examples illustrate the potential of this interface.
Vector field reconstruction from sparse samples with applications
Sibgrapi 2006 (XIX Brazilian Symposium on Computer Graphics and Image Processing): pp. 297-304 (october 2006)
Abstract: This work presents a novel algorithm for 2D vector field reconstruction from sparse set of points-vectors pairs. Our approach subdivides the domain adaptively in order to make local piecewise polynomial approximations for the field. It uses partition of unity to blend those local approximations together, generating a global approximation for the field. The flexibility of this scheme allows handling data from very different sources. In particular, this work presents important applications of the proposed method to velocity and acceleration fields analysis, in particular for fluid dynamics visualization.
Parabolic polygons and discrete affine geometry
Sibgrapi 2006 (XIX Brazilian Symposium on Computer Graphics and Image Processing): pp. 19-26 (october 2006)
Selected for publication in the Journal of Mathematical Imaging and Vision
Selected for publication in the Journal of Mathematical Imaging and Vision
Abstract: Geometry processing applications estimate the local geometry of objects using information localized at points. They usually consider information about the normal as a side product of the points coordinates. This work proposes parabolic polygons as a model for discrete curves, which intrinsically combines points and normals. This model is naturally affine invariant, which makes it particularly adapted to computer vision applications. This work introduces estimators for affine length and curvature on this discrete model and presents, as a proof-of-concept, an affine invariant curve reconstruction.
Competing fronts for coarse-to-fine surface reconstruction
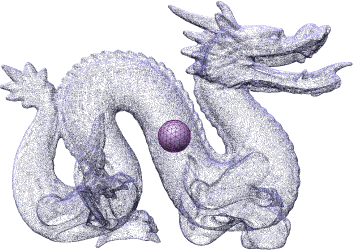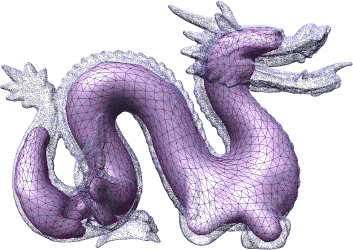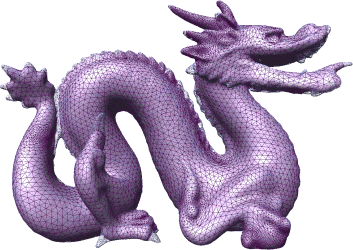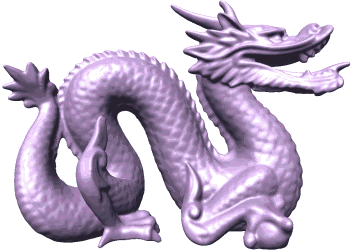
Abstract: This work presents a deformable model to reconstruct a surface from a point cloud. The model is based on an explicit mesh representation composed of multiple competing evolving fronts. These fronts adapt to the local feature size of the target shape in a coarse-to-fine manner. Hence, they approach towards the finer (local) features of the target shape only after the reconstruction of the coarse (global) features has been completed. This conservative approach leads to a better control and interpretation of the reconstructed topology. The use of an explicit representation for the deformable model guarantees water-tightness and simple tracking of topological events. Furthermore, the coarse-to-fine nature of reconstruction enables adaptive handling of non-homogenous sample density, including robustness to missing data in defected areas.
Extraction and compression of hierarchical isocontours from image data
Computerized Medical Imaging and Graphics 30(4): pp. 231-242 (october 2006)
Selected for publication from the Sibgrapi 2004 conference
Selected for publication from the Sibgrapi 2004 conference
Abstract: In this work, we introduce a new scheme to extract hierarchical isocontours from regular and irregular 2D sampled data and to encode it at single rate or progressively. A dynamic tessellation is used to represent and adapt the 2D data to the isocontour. This adaptation induces a controlled multi-resolution representation of the isocontour. This representation can then be encoded while controlling the geometry and topology of the decoded isocontour. The resulting algorithms form an efficient and flexible isocontour extraction and compression scheme.
Mesh compression from geometry
PhD Thesis (december 2005)
directed by Jean--Daniel Boissonnat
directed by Jean--Daniel Boissonnat
Abstract: Images invaded most of contemporary publications and communications. This expansion has accelerated with the development of efficient schemes dedicated to image compression. Nowadays, the image creation process relies on multidimensional objects generated from computer aided design, physical simulations, data representation or optimization problem solutions. This variety of sources motivates the design of compression schemes adapted to specific class of models. This work introduces two compression schemes for geometrical models. The first one encodes level sets in any dimension, in a direct or progressive manner, with both state of the art compression ratios for low dimensions. The second one encodes meshes of any dimension and topology, even non--pure or non-manifold models, embedded in arbitrary space. The compression ratios for surfaces are comparable with famous mesh compression methods such as the Edgebreaker.
Geometric discrete Morse complexes
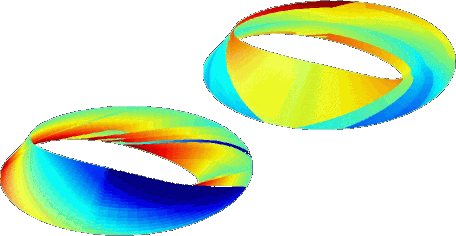
Abstract: Differential geometry provides an intuitive way of understanding smooth objects in the space. However, with the evolution of geometric modeling by computer, this tool became both necessary and difficult to transpose to the discrete setting. The power of Morse theory relies on the link it created between differential topology and geometry. Starting from a combinatorial point of view, Forman s discrete Morse theory relates rigorously discrete objects to their topology, opening Morse theory to discrete structures. This work proposes a constructive definition of geometric discrete Morse functions and their corresponding discrete Morse-Smale complexes, where the geometry is defined as a smooth function sampled on the vertices of the discrete structure. This construction required some homology computations that turned out to be a significant improvement over existing methods by itself. The resulting Morse-Smale decomposition can then be efficiently computed, and used for applications to persistence computation, Reeb graph generation, noise removal...
GEncode: geometry-driven compression in arbitrary dimension and co-dimension
Sibgrapi 2005 (XVIII Brazilian Symposium on Computer Graphics and Image Processing): pp. 249-256 (october 2005)
Selected for publication in Computer Graphics Forum
Selected for publication in Computer Graphics Forum
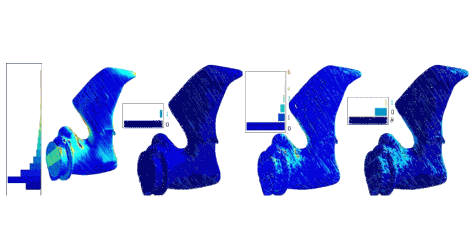
Abstract: Among the mesh compression algorithms, different schemes compress better specific categories of model. In particular, geometry-driven approaches have shown outstanding performances on isosurfaces. It would be expected these algorithm to also encode well meshes reconstructed from the geometry, or optimized by a geometric re-meshing. GEncode is a new single-rate compression scheme that compresses the connectivity of these meshes at almost zero-cost. It improves existing geometry-driven schemes for general meshes on both geometry and connectivity compression. This scheme extends naturally to meshes of arbitrary dimensions in arbitrary ambient space, and deals gracefully with non-manifold meshes. Compression results for surfaces are competitive with existing schemes.
Curvature motion for union of balls
Sibgrapi 2005 (XVIII Brazilian Symposium on Computer Graphics and Image Processing): pp. 47-54 (october 2005)
Abstract: This work proposes a scheme for multi-resolution representation of union of balls in the plane. This representation is inspired by curvature motion for smooth curves. More precisely, the proposed evolution of centers and radii of the balls are based on equations of evolution of the medial axis of a curve that performs curvature motion. The results obtained are very close to the pixel approximation of curvature motion.
CHF: a scalable topological data structure for tetrahedral meshes
Sibgrapi 2005 (XVIII Brazilian Symposium on Computer Graphics and Image Processing): pp. 349-356 (october 2005)
Check also the technical report CHE: A scalable topological data structure for triangular meshes.
Check also the technical report CHE: A scalable topological data structure for triangular meshes.
Abstract: This work introduces a scalable topological data structure for tetrahedral meshes called Compact Half-Face (CHF). It provides a high degree of scalability, which means it is able to optimize the memory consumption / execution time ratio for different applications and data. An object-oriented API using class inheritance and virtual instantiation enables a unique and simple interface of the same functions for every scale. CHF is very concise, simple to implement and easy to use, since it substitutes pointers by container of integers and basic bitwise rules. In particular, the present proposal for CHF s implementation uses generic containers as the one of the C++ Standard Template library (STL).
Curvature and torsion estimators based on parametric curve fitting
Computers & Graphics 29(5): pp. 641-655 (october 2005)
Selected for publication from the Sibgrapi 2004 conference. Check also the technical report Least Squares Estimation of Curvature and Torsion.
Selected for publication from the Sibgrapi 2004 conference. Check also the technical report Least Squares Estimation of Curvature and Torsion.
Abstract: Many applications of geometry processing and computer vision rely on geometric properties of curves, particularly their curvature. Several methods have already been proposed to estimate the curvature of a planar curve, most of them for curves in digital spaces. This work proposes a new scheme for estimating curvature and torsion of planar and spatial curves, based on weighted least-squares fitting and local arc-length approximation. The method is simple enough to admit a convergence analysis that takes into account the effect of noise in the samples. The implementation of the method is compared to other curvature estimation methods showing a good performance. Applications to prediction in geometry compression are presented both as a practical application and as a validation of this new scheme.
Simplicial isosurface compression
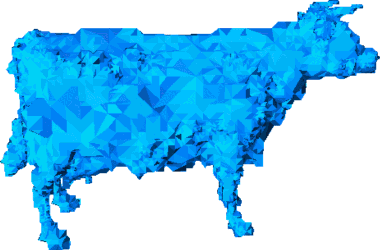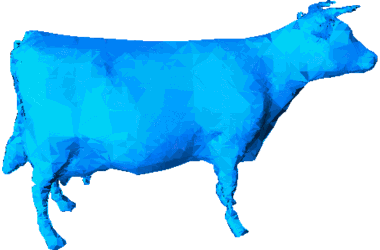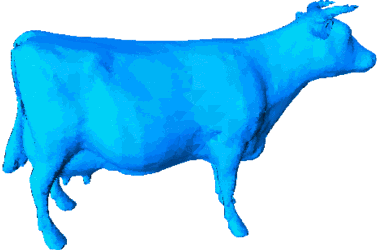
Abstract: In this work, we introduce a new algorithm for direct and progressive encoding of isosurfaces extracted from volumetric data. A binary multi-triangulation is used to represent and adapt the 3D scalar grid. This simplicial scheme provides geometrical and topological control on the decoded isosurface. The resulting algorithm is an efficient and flexible isosurface compression scheme.
Stellar mesh simplification using probabilistic optimization
Computer Graphics Forum 23(4): pp. 825-838 (october 2004)
Selected for publication from the Sibgrapi 2003 conference
Selected for publication from the Sibgrapi 2003 conference
Abstract: This paper proposes the Fast Stellar mesh simplification, a fast implementation of the Four-Face Cluster algorithm. In this method, a probabilistic optimization heuristic substitutes the priority queue of the original Four-Face Cluster, which results in a 40% faster algorithm with the same order of distortion. It extends naturally to a progressive and/or multi-resolution scheme for combinatorial surfaces This work also presents a simple way to encode the hierarchy of the multi-resolution meshes. A very significant objective of this work is to point out important aspects to be considered when developing a practical and robust implementation of this simplification technique, and analyses the influence of the parameters.
Efficient EdgeBreaker for surfaces of arbitrary topology
Sibgrapi 2004 (XVII Brazilian Symposium on Computer Graphics and Image Processing): pp. 218-225 (october 2004)
Abstract: The typical surfaces models handled by contemporary Computer Graphics applications have millions of triangles and numerous connected component, handles and boundaries. Edgebreaker and Spirale Reversi are examples of efficient schemes to compress and decompress their connectivity. A surprisingly simple linear-time implementation has been proposed for triangulated surfaces homeomorphic to a sphere and was subsequently extended to surfaces with handles.
Arc-length based curvature estimator
Sibgrapi 2004 (XVII Brazilian Symposium on Computer Graphics and Image Processing): pp. 250-257 (october 2004)
Selected for publication in Computers & Graphics
Selected for publication in Computers & Graphics
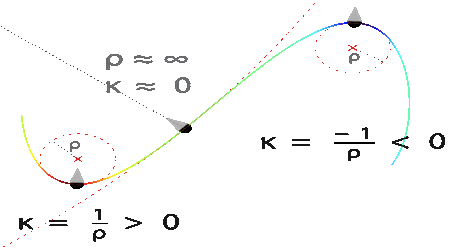
Abstract: Many applications of geometry processing and computer vision rely on geometric properties of curves, particularly their curvature. Several methods have been proposed to estimate the curvature of a planar curve, most of them for curves in digital spaces. This work proposes a new method for curvature estimation based on weighted least square fitting and local arc-length approximation. Convergence analysis of this method and noise impact on the estimator accuracy are given. Numerical robustness issues are addressed with practical solutions. The implementation of the method is compared to other curvature estimation methods.
Hierarchical isocontours extraction and compression
Sibgrapi 2004 (XVII Brazilian Symposium on Computer Graphics and Image Processing): pp. 234-241 (october 2004)
Selected for publication in Computerized Medical Imaging and Graphics
Selected for publication in Computerized Medical Imaging and Graphics
Abstract: In this work, we introduce a new scheme to extract hierarchical isocontours from regular and irregular 2D sampled data and to encode it at single rate or progressively. A dynamic tessellation is used to represent and adapt the 2D data to the isocontour. This adaptation induces a controlled multi-resolution representation of the isocontour. We can then encode this representation and control the geometry and topology of the decoded isocontour. The resulting algorithms form an efficient and flexible isocontour extraction and compression scheme.
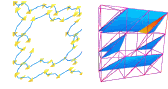
Applications of Forman s discrete morse theory to topology visualization and mesh compression
Transactions on Visualization and Computer Graphics 10(5): pp. 499-508 (september 2004)
Selected for publication from the Visualization and Mathematics 2002 conference
Selected for publication from the Visualization and Mathematics 2002 conference
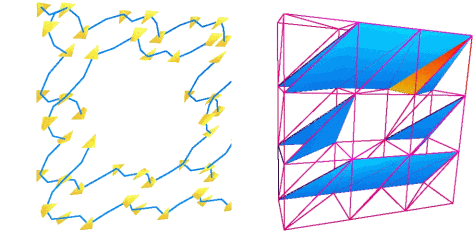
Abstract: Morse theory is a powerful tool for investigating the topology of smooth manifolds. It has been widely used by the computational topology, computer graphics and geometric modeling communities to devise topology based algorithms and data structures. Forman introduced a discrete version of this theory, which is purely combinatorial. This paper aims at building, visualizing and applying the basic elements of Forman s discrete Morse theory. It intends to use some of these concepts to visually study the topology of an object. As a basis, an algorithmic construction of optimal Forman s discrete gradient vector fields is provided. This construction is then used to topologically analyze mesh compression schemes, such as Edgebreaker and Grow&Fold. In particular, this paper proves that the complexity class of the strategy optimization of Grow&Fold is MAX-SNP hard.
Fast stellar mesh simplification
Sibgrapi 2003 (XVI Brazilian Symposium on Computer Graphics and Image Processing): pp. 27-34 (october 2003)
Selected for publication in Computer Graphics Forum
Selected for publication in Computer Graphics Forum
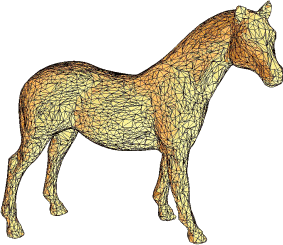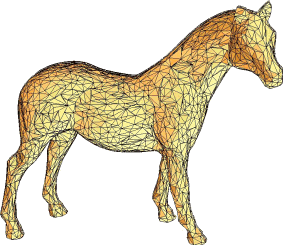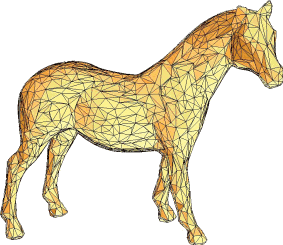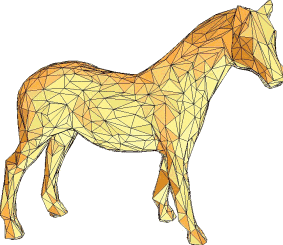
Abstract: This paper introduces Stellar Simplification, a fast implementation of the Four-Face Cluster algorithm. In our version of this mesh simplification scheme, we adopt a probabilistic heuristic that substitutes the priority queue of the original algorithm. This made our version, in average, 40% faster. In our implementation, we adopt a very concise data structure that uses only two arrays of integers to represent the surface topology. We also introduce a new scheme to encode and decode the hierarchy of meshes generated by the simplification algorithm. This scheme can be used for progressive transmission and compression of meshes.
Molecular shape analysis based upon Morse-Smale complex and the connolly function
Abstract: Docking is the process by which two or several molecules form a complex. Docking involves the geometry of the molecular surfaces, as well as chemical and energetic considerations. In the mid-eighties, Connolly proposed a docking algorithm matching surface knobs with surface depressions. We recast the notions of knob and depression of the Connolly function in the framework of Morse theory for functions defined over two-dimensional manifolds. First, we study the critical points of the Connolly function for smooth surfaces. Second, we provide an efficient algorithm for computing the Connolly function over a triangulated surface. Third, we introduce a Morse-Smale decomposition based on Forman s discrete Morse theory, and provide an O(n.log n) algorithm to construct it. This decomposition induces a partition of the surface into regions of homogeneous flow, and provides an elegant way to relate local quantities to global ones -from critical points to Euler characteristic of the surface. Fourth, we apply this Morse-Smale decomposition to the discrete gradient vector field induced by Connolly s function, and present experimental results for several mesh models.
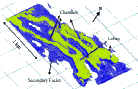
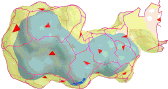
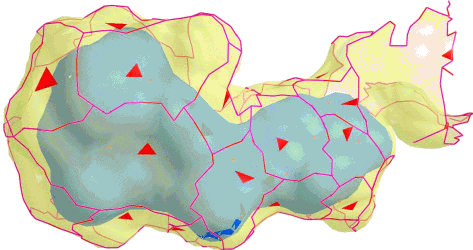
Topological reconstruction of oil reservoirs from seismic surfaces
International Association for Mathematical Geology (september 2003)
Abstract: The characterization of oil reservoirs has as one of its components the study of their geometry and topology. While the geometry deals with spatial distribution of points and its associated properties, e.g. permeability and porosity, the topology handles its connectivity. One of the main characteristics of seismic processing is the generation of large data sets. Computationally intensive powerful techniques are needed to extract meaningful information from these data. The main objective of the talk will be to show how to reconstruct geological objects (channels, lobes, etc.) directly from seismic data. The data is piled up in offset groups in such a way as to get information from the seismic aiming at the geological modeling.
Efficient implementation of marching cubes cases with topological guarantees
Abstract: Marching Cubes methods first offered visual access to experimental and theoretical data. This method s implementation usually relies on a small lookup table. Many enhancements and optimizations of this method still use it. However, this lookup table can lead to cracks and inconsistent topology. This paper introduces a full implementation of Chernyaev s Marching Cubes 33 method to ensure a topologically correct result. It completes the original paper for the ambiguity resolution and for the feasibility of the implementation.
Towards optimality in discrete Morse theory
Abstract: Morse theory is a fundamental tool for investigating the topology of smooth manifolds. This tool has been extended to discrete structures by Forman, which allows combinatorial analysis and direct computation. This theory relies on discrete gradient vector fields, whose critical elements describe the topology of the structure. The purpose of this work is to construct optimal discrete gradient vector fields, where optimality means having the minimum number of critical elements. The problem is equivalently stated in terms of maximal hyperforests of hypergraphs. Deduced from this theoretical result, a construction algorithm is provided. The optimal parts are proved, and the part of exponential complexity is replaced by heuristics. Although reaching optimality is MAX-SNP hard, the experiments on odd topological models are almost optimal.
Constructing discrete Morse functions
Master Thesis (july 2002)
(also available in Portuguese, and in a short version presented at the Sibgrapi 2003 WTD)
(also available in Portuguese, and in a short version presented at the Sibgrapi 2003 WTD)
Abstract: This work aims to study optimality in discrete Morse functions on general cell complex, where optimality entails having the least number of critical elements. This problem is proven here to be MAX-SNP hard. However, we provide a linear algorithm that, for the case of 2-manifolds, always reaches optimality. We prove here various results on the structure of a discrete Morse function. In particular, we provide an equivalent representation by hyperforests. From this point of view, we designed a construction of discrete Morse functions for general cell complexes of arbitrary finite dimension. The resulting algorithm is quadratic in time and, although not guaranteed to be optimal, gives optimal answers in most of the practical cases.
Visualizing Forman s discrete vector field
Visualization and Mathematics III (VisMath 2002): pp. 95-112 (may 2002)
Selected for publication in IEEE TVCG
Selected for publication in IEEE TVCG
Abstract: Morse theory has been considered to be a powerful tool in its applications to computational topology, computer graphics and geometric modeling. Forman introduced a discrete version of it, which is purely combinatorial. This opens Morse theory applications to a much larger scope. The main objective of this work is to illustrate Forman s theory. We intend to use some of Forman s concepts to visually analyze the topology of an object. We present an algorithm to build a Morse-Forman s discrete gradient vector field on a cell complex.
Optimal discrete Morse functions for 2-manifolds
Abstract: Morse theory was originally formulated for smooth manifolds. Recently, Robin Forman formulated a version of this theory for discrete structures such as cell complexes. It opens up several categories of interesting objects (particularly meshes) to applications of Morse theory. Once a Morse function has been defined on a manifold, then information about its topology can be deduced from its critical elements. This paper introduces a linear algorithm to define optimal discrete Morse functions on discrete 2-manifolds, where optimality entails having the least number of critical elements. The algorithm presented is also extended to general finite cell complexes of dimension at most 2, with no guarantee of optimality.
Projects
- FAPERJ - Jovem Cientísta do Nosso Estado (2016-2019): Projeto de pesquisa sobre reconhecimento de gestos e sinais.
- FAPERJ - Iniciação Científica (2013-2014): Bolsa de iniciação científica para Anna Lívia Souza sobre o tema: Medição sísmica na presença de ondas marítimas.
- CAPES - PAEP, FAPERJ - APQ2, INCT Mat, CNPq - ARC e Springer: Apoio ao SocG 2013.
- FAPERJ - Jovem Cientísta do Nosso Estado (2012-2015): Projeto de pesquisa sobre geometria e topologia discretas.
- FAPERJ - Estágio de Doutorando no exterior (2012.2): Apoio ao estágio de doutorado do aluno João Paixã na Universidade de Queensland (Austrália), sobre a supervisão de Benjamin Burton.
- FAPERJ - Estágio de Doutorando no exterior (2012.1): Apoio ao estágio de doutorado da aluna Renata Nascimento no INRIA (França), sobre a supervisão de Pierre Alliez.
- Bolsa de pesquisador CNPq - nível 1D (2011-2014): Projeto de pesquisa sobre modelagem geométrica discreta.
- MCT/CNPq - Universal (coordenador) (2010-2011): Projeto de pesquisa sobre superfícies discretas em evolução.
- CNPq - Bolsa de Mestrado (2009-2011): Bolsa de Mestrado sobre superfícies implícitas e visualização.
- CNPq - ARC, CAPES - PAEP, Petrobras, FAPERJ - APQ2, INCT Mat, PUC-Rio and UFF: Apoio ao Sibgrapi 2009.
- FAPERJ - Jovem Cientísta do Nosso Estado (2009-2012): Projeto de pesquisa sobre reconstrução de objetos geométricos.
- ARCUS (2008-2010): Projeto de colaboração internacional região Rhône-Alpes - Brasil, entre a Universidade Joseph Fourier de Grenoble et a PUC-Rio.
- Bolsa de pesquisador CNPq - nível 2 (2008-2010): Projeto de pesquisa sobre reconstrução de objetos 3D.
- MCT/CNPq - Universal (2008-2009): Projeto de pesquisa sobre dinâmica e geometria estocástica de objetos pontuais com aplicações à geologia de fraturas.
- FAPERJ - Pensa Rio (2008-2009): Projeto de pesquisa ModFin, para desenvolver um software para modelagem, simulação e geração de cenários financeiros e macroeconômicos com aplicação para sistemas ALM.
- MCT/CNPq - Universal (coordenador) (2007-2008): Projeto de pesquisa sobre compressão de objetos tridimensionais, do ponto de vista geométrico e combinatório.
- MCT/CNPq - Universal (2007-2008): Projeto de pesquisa sobre geometrias euclidianas, afins e projetivas de curvas discretas.
- INRIA / CNPq (2005-2008): Projeto de colaboração internacional CNPq-INRIA, envolvendo o departamento de Matemática da PUC-Rio ao projeto Géométrica do INRIA de Sophia Antipolis.
- Dinâmica da Estruturação Salífera (Desde 2011) - Petrobras (petróleo): análise, simulações numéricas e visualização dos estados termo-mecânicos do sal.
- Fluidos turbiditos (2006-2010) - Petrobras (petróleo): simulação de fluidos multifásicos.
- KernelSis (2007-2009) - Petrobras (petróleo): aprendizagem conjunta de dados sísmicos com dados de poço.
- MultiFacis (2007-2008) - Petrobras (petróleo): análise e visualização de dados sísmicos com multi-atributos.
- Pigalyse (2007-2008) - CPTI (instrumentação): reconstrução a partir de feixes de ultra-sons oblíquos.
- Petbool (2007) - Petrobras (petróleo): modelagem geológica estochástica de reservatórios.
- Geosis (2004 - 2008) - Petrobras (petróleo): reconstrução de dados sísmicos com multi-atributos.
- Poros (Agosto-Dezembro 2003) - Petrobras (petróleo): simulador de meios porosos.
- SiniPrev (Julho-Agosto 2002) - Bradesco seguros (seguro): análise de ocorrência de sinistros.
- Geosis (Agosto-Setembro 2002) - Petrobras (petróleo): reconstrução de superfícies a partir de dados sísmicos.
- Sirrocco (Fevereiro-Junho 2001) - Telecom ParisTech (telecomunicações): perfect hashing para organização de dicionários.
Colegas
- Álvaro Veiga: Departamento de Engenharia Eletrica, PUC-Rio.
- Adelailson Peixoto: Departamento de Matemática, Universidade Federal de Alagoas.
- Afonso Paiva Neto: ICMC, USP - São Carlos.
- Alex Laier Bordignon: Departamento de Matemática, PUC-Rio.
- Alla Sheffer: Departamento de Informática, UBC.
- Allyson Cabral: Departamento de Matemática, PUC-Rio: aluno de doutorado.
- Americo Barbosa da Cunha Junior: Departamento de Engenharia Mecânica, PUC-Rio: aluno de projeto final de graduação.
- Andrei Sharf: Departamento de Informática, Universidade Ben-Gurion.
- Anna Lívia Souza: CEFET - RJ: aluna de iniciação científica (PICME).
- Antônio Wilson Vieira: Unimontes.
- Antonio Claudio Soares: CENPES, Petrobras.
- Ariel Shamir: Departamento de Informática, Centro Interdisciplinário de Herzliya.
- Armando Prestes: SINTEF Brasil.
- Arthur Kölblinger: CEFET - RJ: aluno de iniciação científica (PICME).
- Benjamin A. Burton: School of Mathematics and Physics, the University of Queensland.
- Bernardo Ribeiro: Colégio Dom Pedro II: aluno de iniciação científica.
- Betina Vath: Departamento de Engenharia do Petróleo, UFF: aluna de mestrado (dissertação).
- Bianca Lodoli: IME: aluno de iniciação científica (PICME).
- Carlos Simonsen Leal: Departamento de Matemática, UFRJ: aluno de iniciação científica.
- Catiuscia Borges: Escola Jockey Club Brasileiro: aluna de mestrado (dissertação).
- Chen Greif: Departamento de Informática, UBC.
- Clarissa Codá Marques: Departamento de Matemática, PUC-Rio: aluna de doutorado (tese).
- Cynthia Oliveira Lage Ferreira: ICMC, USP - São Carlos.
- Dan Alcantara: Departamento de Informática, UC Davis.
- Daniel Cohen-Or: Departamento de Informática, Universidade de Tel Aviv.
- Daniel Fleischman: Cornell University: aluno de projeto final de graduação.
- David Cohen-Steiner: Projeto Géométrica, INRIA - Sophia Antipolis.
- David Rey: LICIT, INRETS: aluno de mestrado (dissertação).
- Dimas Martinez Morera: Departamento de Matemática, Universidade Federal de Alagoas.
- Eliton Filho: IME: aluno de iniciação científica (PICME).
- Eric Cardona Romani: Departamento de Física, PUC-Rio: aluno de projeto final de graduação.
- Eric Fusy: LIX, Ecole Polytechnique.
- Erick Costa e Silva Talarico: Petrobras: aluno de iniciação científica.
- Esdras Medeiros: Departamento de Matemática, Universidade Federal do Ceará.
- Esteban Clua: Departamento de Informática, UFF.
- Fabiano Petronetto do Carmo: Departamento de Matemática, Federal University of Espírito Santo.
- Frédéric Cazals: Projeto ABS, INRIA - Sophia Antipolis.
- Frédéric Chazal: Projeto Géométrica, INRIA - Saclay.
- Günter Ziegler: Projeto Matheon, Technische Universität Berlin.
- Geovan Tavares: Departamento de Matemática, PUC-Rio.
- Gil Shklarski: Microsoft Redmond.
- Guilherme Dias da Fonseca: .
- Hélio Lopes: Departamento de Matemática, PUC-Rio: orientador de Mestrado e de Doutorado.
- Henri Anciaux: Instituto de Matemática e Estatística, USP.
- I-Shih Liu: Instituto de Matemática, UFRJ.
- Jarek Rossignac: Colégio de Informática, Georgia Tech.
- Jean-Daniel Boissonnat: Projeto Géométrica, INRIA - Sophia Antipolis: orientador de Doutorado.
- Jean-Marie Morvan: Instituto Camille Jordan, Universidade Claude Bernard Lyon.
- João Domingos Gomes: .
- João Luiz Campos: TecGraf, PUC-Rio.
- João Paixão: Departamento de Ciêcia da Computação, UFRJ: aluno de mestrado (dissertação) e de doutorado.
- Jonathan Spreer: School of Mathematics and Physics, the University of Queensland.
- Jyrko Correa Morris: Departamento de Matemática, PUC-Rio: aluno de doutorado (tese).
- Karen Carilho: Departamento de Matemática, PUC-Rio: aluno de doutorado.
- Karine Pereira: Departamento de Matemática, PUC-Rio: aluna de mestrado.
- Konrad Polthier: Projeto Matheon, Freie Universität Berlin.
- Leandro Lopes: IME: aluno de iniciação científica (PICME).
- Leandro Miranda: Departamento de Matemática, Universidade Federal de Alagoas.
- Leif Kobbelt: Departamento de Informática, RWTH Aachen.
- Lis Custódio: Departamento de Matemática, PUC-Rio: aluna de mestrado (dissertação).
- Luca Castelli Aleardi: LIX, Ecole Polytechnique.
- Lucas Mauricio Sigaud: Departamento de Física, PUC-Rio.
- Lucas von Haehling Braune: Departamento de Matemática, PUC-Rio: aluno de iniciação científica (relatório).
- Luis Peñaranda: Departamento de Ciêcia da Computação, UFRJ.
- Luiz Henrique de Figueiredo: Laboratório VISGRAF, IMPA.
- Luiz Palermo: CENPES, Petrobras.
- Luiz Velho: Laboratório VISGRAF, IMPA.
- Mário Fernando Montenegro Campos: Departamento de Ciência da Computação, UFMG.
- Marcelo Dreux: Departamento de Engenharia Mecânica, PUC-Rio.
- Marcos Craizer: Departamento de Matemática, PUC-Rio.
- Marcos Oliveira Lage Ferreira: Departamento de Informática, UFF.
- Maria de Andrade: Departamento de Matemática, Universidade Federal de Alagoas: aluna de doutorado (tese).
- Mariana Milazzo: Colégio Dom Pedro II: aluna de iniciação científica.
- Marina Dias: Departamento de Matemática, PUC-Rio.
- Mario Fernando Montenegro Campos: Departamento de Ciência da Computação, UFMG.
- Matheus Felipe Ferreira Maciel: Departamento de Informática, PUC-Rio: aluno de iniciação científica.
- Mauro Antonio Rincon: Instituto de Matemática, UFRJ.
- Moacyr Alvim Barbosa: Fondação Getulio Vargas.
- Nina Amenta: Departamento de Informática, UC Davis.
- Paulo Paraizo: CENPES, Petrobras.
- Pierre Alliez: Projeto Géométrica, INRIA - Sophia Antipolis.
- Rafael Cação: IME: aluno de iniciação científica (PICME).
- Rafael Lassance de Oliveira Alonso Martinez: Departamento de Matemática, PUC-Rio: aluno de iniciação científica e mestrado.
- Raffael Capano de Arruda: Departamento de Informática, PUC-Rio: aluno de iniciação científica.
- Ralph Costa Teixeira: Instituto de Matemática, UFF.
- Renata Nascimento: Departamento de Matemática, PUC-Rio: aluna de mestrado (dissertação) e de doutorado.
- Renato Paes Leme: Google Research New York.
- Rener Pereira de Castro: Banco Itaú: aluno de doutorado (tese).
- Ricardo da Silva Torres: Instituto de Computação, Unicamp.
- Rodrigo de Toledo: Departamento de Ciêcia da Computação, UFRJ.
- Rogério Santos: Internacional, Petrobras.
- Roger Véron: Departamento de Matemática, PUC-Rio: aluno de doutorado.
- Rolci Cipolatti: Instituto de Matemática, UFRJ.
- Romulo Brito: Departamento de Computação, UFRJ: aluna de mestrado (dissertação).
- Scarlett de Botton: .
- Sinésio Pesco: Departamento de Matemática, PUC-Rio.
- Sivan Toledo: Departamento de Informática, Universidade de Tel Aviv.
- Thales Vieira: Departamento de Matemática, Universidade Federal de Alagoas: aluno de mestrado (dissertação) e de doutorado (tese).
- Thiago Pereira: Princeton University.
- Victor Hugo de Oliveira: IME: aluno de iniciação científica (PICME).
- Vinícius Mello: Departamento de Matemática, Universidade Federal de Bahia.
- Welles A.M. Morgado: Departamento de Física, PUC-Rio.
- William Robson Schwartz: Departamento de Ciência da Computação, UFMG.
Ensino
- MAT2464 (2015.1): Introduçã à topologia computacional (curso de pós-graduação em Matemática).
- MAT1200 (2015.1): Álgbra linear I, coordenador (ciclo básico do Centro Técnico Científico).
- MAT1200 (2014.2): Álgbra linear I, coordenador (ciclo básico do Centro Técnico Científico).
- MAT1305/MAT2462 (2014.2): Modelagem geométrica (curso de graduação e pós-graduação em Matemática).
- MAT1200 (2014.1): Álgbra linear I, coordenador (ciclo básico do Centro Técnico Científico).
- MAT1231/MAT2229 (2014.1): Álgbra linear numérica (curso de graduação e pós-graduação em Matemática).
- MAT1305/MAT2462 (2013.2): Modelagem geométrica (curso de graduação e pós-graduação em Matemática).
- MAT1310 (2013.2): Matemática discreta (ciclo básico do Centro Técnico Científico).
- MAT2465 (2013.1): Geometria discreta e computacional (curso de pós-graduação em Matemática).
- MAT1231/MAT2229 (2013.1): Álgbra linear numérica (curso de graduação e pós-graduação em Matemática).
- MAT1406/MAT2447 (2012.2): Métodos Numéricos em Equações Diferenciais (curso de graduação e pós-graduação em Matemática).
- MAT1305/MAT2442 (2012.1): Modelagem geométrica (curso de graduação e pós-graduação em Matemática).
- MAT1301 (2012.1): Elementos Matemáticos para Computação Gráfica (curso de graduação e pós-graduação em Matemática).
- MAT1231/MAT2229 (2012.1): Álgbra linear numérica (curso de graduação e pós-graduação em Matemática).
- Topologia das variedades (e não variedades) discretas com complexos celulares: mini-curso no trimestre temático sobre variedades computacionais e aplicações (IMPA).
- MAT1406/MAT2447 (2011.2): Métodos Numéricos em Equações Diferenciais (curso de graduação e pós-graduação em Matemática).
- MAT1310 (2011.2): Matemática discreta, coordenador (ciclo básico do Centro Técnico Científico).
- Cálculo e Estimação de Invariantes Geométricos - Uma Introdução às Geometrias Euclidiana e Afim., avec Maria Andrade (08/2011): Curso avançado do 28o Colóquio Brasileiro de Matemática, no IMPA.
- Fundamentos matemáticos para o processamento de imagens (2011.1): Introdução ao processamento de imagens (curso de bacharelado e pós-graduação em Matemática).
- MAT1310 (2011.1): Matemática discreta, coordenador (ciclo básico do Centro Técnico Científico).
- Curvas e Superfícies Implícitas: Noções de Geometria Diferencial e Discreta , com Maria Andrade, Allyson Cabral, Vinícius Mello et Adelailson Peixoto (03/2011): mini-curso do 1o Colóquio de Matemática do Nordeste.
- Reconstrução (2010.2): Métodos de Reconstrução 3D (curso de pós-graduação em Matemática).
- MAT1310 (2010.2): Matemática discreta, coordenador (ciclo básico do Centro Técnico Científico).
- Topologia computacional (2010.1): introdução às topologias algébricas e combinatórias, com suas versões computacionais (curso de pós-graduação em Matemática).
- MAT1071 (2010.1): Curso de Matemática do Espaço e das Formas, usando Google Sketch'Up, para os alunos do primeiro ano no Departamento de Arquitetura e Urbanismo da PUC-Rio.
- MAT1305/MAT2442 (2009.2): Modelagem geométrica (curso de graduação e pós-graduação em Matemática).
- MAT1071 (2009.2): Curso de Matemática do Espaço e das Formas para os alunos do primeiro ano no Departamento de Arquitetura e Urbanismo da PUC-Rio.
- MAT1161 (2009.2): Cálculo a uma Variável, laboratório de Maple (ciclo básico do Centro Técnico Científico).
- Simulação de fluidos sem malha, uma introdução ao método SPH, com Afonso Paiva, Fabiano Petronetto e Geovan Tavares (08/2009): Curso introdutório do 27o Colóquio Brasileiro de Matemática, no IMPA.
- MAT1072 (2009.1): Curso de C´lculo para os alunos do segundo ano no Departamento de Arquitetura e Urbanismo da PUC-Rio.
- MAT1071 (2009.1): Curso de Matemática do Espaço e das Formas para os alunos do primeiro ano no Departamento de Arquitetura e Urbanismo da PUC-Rio.
- MAT1161 (2009.1): Cálculo a uma Variável, laboratório de Maple (ciclo básico do Centro Técnico Científico).
- Introdução à Computação Gráfica, junto com Vinícius Mello (01-02/2009): Curso no programa de verão da Universidade Federal de Alagoas.
- Superfícies implícitas e isosuperfícies: dos cursos de cálculo até as indústrias médicas, de jogos e do petróleo, junto com Adelailson Peixoto (11/2008): Minicurso oeferecido no IV Simpósio Nacional / Jornadas de Iniciação Científica do IMPA.
- Modelagem avançada (2008.2): avanços em modelagem geométrica de 1990 a 2008 (curso de pós-graduação em Matemática).
- MAT1153 (2008.2): Cálculo Integral a Várias Variáveis, coordenador (ciclo básico do Centro Técnico Científico).
- MAT1153 (2008.1): Cálculo Integral a Várias Variáveis, coordenador (ciclo básico do Centro Técnico Científico).
- Reconstrução (2007.2): Métodos de Reconstrução 3D (curso livre com Luiz Velho e Dimas Martinez Morera, ministrado no IMPA).
- Compressão 3D: de A a Zip (10/2007): Tutorial oferecido durante o Sibgrapi 2007.
- MAT1610/MAT2620 (2007.2): Análise na reta (curso de graduação e pós-graduação em Matemática).
- MAT1153m (2007.2): Cálculo Integral a Várias Variáveis com Maple (ciclo básico do Centro Técnico Científico).
- MAT1301 (2007.1): Elementos Matemáticos para Computação Gráfica (curso de graduação e pós-graduação em Matemática).
- MAT1151 (2007.1): Cálculo a uma Variável, laboratório de Maple (ciclo básico do Centro Técnico Científico).
- MAT2413 (2006.2): Teoria das distribuições (curso de pós-graduação em Matemática).
- MAT1172 (2006.2): Cálculo Diferencial a Várias Variáveis, turma especial (ciclo básico do Centro Técnico Científico).
- Compressão de objetos 3D (06/2006): Mini-curso da Matfest 2006, da Universidade Federal de Alagoas.
- MAT1153 (2006.1): Cálculo Integral a Várias Variáveis (ciclo básico do Centro Técnico Científico).
- MI1 (2003.2): Aulas práticas de informática do primeiro ano no Departamento de Informática, Universidade de Nice.
- MAT1071 (2002.1): Curso de Matemática do Espaço e das Formas para os alunos do primeiro ano no Departamento de Arquitetura e Urbanismo da PUC-Rio.
Downloads
- Script em bash para criar uma imagem de miniaturas de pdf ou video usando ImageMagick e FFmpeg: para pdfs pdfthumb (3 KB, modificado dia 30/03/2012), e para videos videothumb (3 KB, modificado dia 09/07/2011).
- Código open source do algoritmo Very Simple Volume Rendering para renderizar dados volumétricos: arquivo ZIP (92 KB, modificado dia 16/05/2010).
- Pacote LaTeX simples para inserir imagens: arquivo ZIP (2 KB, modificado dia 07/03/2008).
- Formato LaTeX para as prepublicações do departamento de Matemática da PUC-Rio: arquivo ZIP (580 KB, modificado dia 19/02/2008).
- Formato LaTeX para teses e dissertações da PUC-Rio: arquivo ZIP (619 KB, modificado dia 22/08/2011), em colaboração com Marcelo Roberto Jimenez.
- Código open source do artigo sobre Marching Cubes, com exemplos: arquivo ZIP (166 KB, modificado dia 14/12/2009).
- Programa de demonstração (windows) do artigo sobre a Estimação de curvaturas com o comprimento de arco, com exemplos: arquivo ZIP (611 KB, modificado dia 03/08/2006).
Informações de Contato
- Email: lewiner@gmail.com
- Página Pessoal: thomas.lewiner.org
- Telefone: (021) 3527 1747
- Endereço:
Thomas Lewiner
Departamento de Matemática
Rua Marquês de São Vicente, 225, Gávea
Rio de Janeiro, RJ - 22451.900
Brasil