Parabolic polygons and discrete affine geometry

Parabolic polygons and discrete affine geometry
Marcos Craizer, Thomas Lewiner, Jean-Marie Morvan

Abstract:

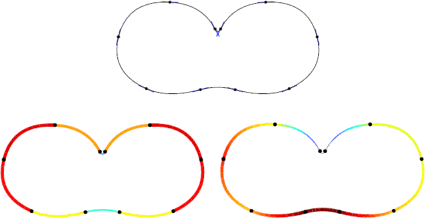
Geometry processing applications estimate the local geometry of objects using information localized at points. They usually consider information about the normal as a side product of the points coordinates. This work proposes parabolic polygons as a model for discrete curves, which intrinsically combines points and normals. This model is naturally affine invariant, which makes it particularly adapted to computer vision applications. This work introduces estimators for affine length and curvature on this discrete model and presents, as a proof-of-concept, an affine invariant curve reconstruction.

Downloads:

PDF paper (371 KB)
PPT presentation (2 MB)

BibTeX:

@inproceedings{parabolic_polygon_sibgrapi,
    author = {Marcos Craizer and Thomas Lewiner and Jean-Marie Morvan},
    title = {Parabolic polygons and discrete affine geometry},
    year = {2006},
    month = {october},
    booktitle = {Sibgrapi 2006 (XIX Brazilian Symposium on Computer Graphics and Image Processing)},
    pages = {19--26},
    publisher = {IEEE},
    address = {Manaus, AM},
    doi = {10.1109/SIBGRAPI.2006.32},
    url = {\url{http://thomas.lewiner.org/pdfs/parabolic_polygon_sibgrapi.pdf}}
}