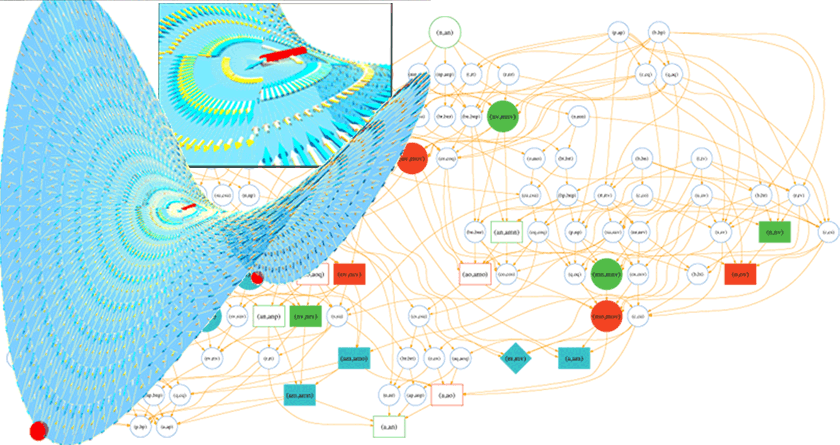
Critical sets in discrete Morse theories: relating Forman and piecewise-linear approaches

Critical sets in discrete Morse theories: relating Forman and piecewise-linear approaches
Thomas Lewiner

Abstract:

Morse theory inspired several robust and well grounded tools in discrete function analysis, geometric modeling and visualization. Such techniques need to adapt the original differential concepts of Morse theory in a discrete setting, generally using either piecewise--linear (PL) approximations or Forman's combinatorial formulation. The former carries the intuition behind Morse critical sets, while the latter avoids numerical integrations. Forman's gradients can be constructed from a scalar function using greedy strategies, although the relation with its PL gradient is not straightforward. This work relates the critical sets of both approaches. It proves that the greedy construction on two-dimensional meshes actually builds an adjacent critical cell for each PL critical vertex. Moreover, the constructed gradient is globally aligned with the PL gradient. Those results allow adapting the many works in PL Morse theory for triangulated surfaces to Forman's combinatorial setting with low algorithmic complexity.

Downloads:

PDF paper (698 KB)

BibTeX:

@article{discrete_critical_set_cagd,
    author = {Thomas Lewiner},
    title = {Critical sets in discrete Morse theories: relating Forman and piecewise-linear approaches},
    year = {2013},
    month = {july},
    journal = {Computer Aided Geometric Design},
    volume = {30},
    number = {6},
    pages = {609--621},
    publisher = {Elsevier},
    doi = {10.1016/j.cagd.2012.03.012},
    url = {\url{http://thomas.lewiner.org/pdfs/discrete_critical_set_cagd.pdf}}
}