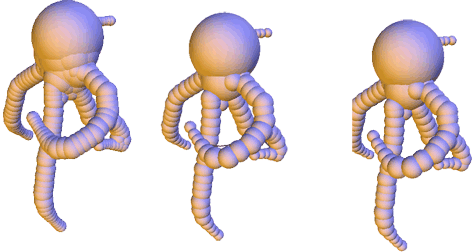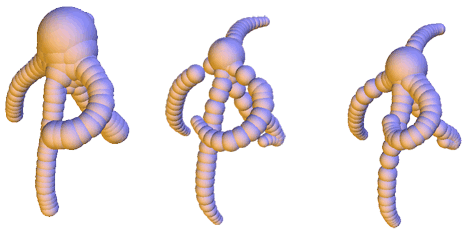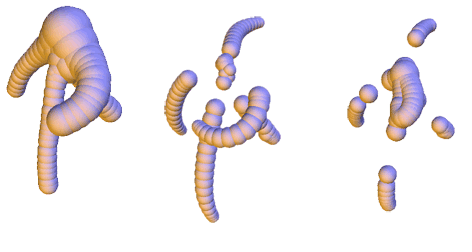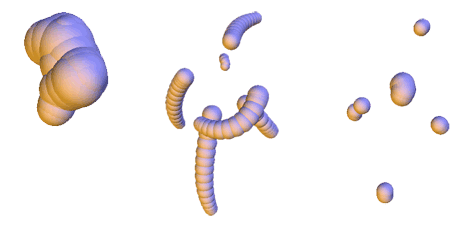
Scale-space for union of 3d balls

Scale-space for union of 3d balls
Alex Bordignon, Betina Vath, Thales Vieira, Cynthia Ferreira, Marcos Craizer, Thomas Lewiner

Abstract:

Shape discretization through union of weighted points or balls appears as a common representation in different fields of computer graphics and geometric modeling. Among others, it has been very successful for implicit surface reconstruction with radial basis functions, molecular atomic models, fluid simulation from particle systems and deformation tracking with particle filters. These representations are commonly generated from real measurements or numerical computations, which may require filtering and smoothing operations. This work proposes a smoothing mechanism for union of balls that tries to inherit from the scale-space properties of bi-dimensional curvature motion: it avoids disconnecting the shape, prevents self-intersection, regularly decreases the area and convexifies the shape. The smoothing is computed iteratively by moving each ball of the union according to a combination of projected planar curvature motions. Experiments exhibits nice properties of this scale-space.

Downloads:

PDF paper (8.3 MB)
Slides in PDF (15.6 MB)
movie (26 MB)
YouTube

BibTeX:

@inproceedings{medialmove3d_sibgrapi,
    author = {Alex Bordignon and Betina Vath and Thales Vieira and Cynthia Ferreira and Marcos Craizer and Thomas Lewiner},
    title = {Scale-space for union of 3d balls},
    year = {2009},
    month = {october},
    booktitle = {Sibgrapi 2009 (XXII Brazilian Symposium on Computer Graphics and Image Processing)},
    pages = {9--16},
    publisher = {IEEE},
    address = {Rio de Janeiro, RJ},
    doi = {10.1109/Sibgrapi.2009.9},
    url = {\url{http://thomas.lewiner.org/pdfs/medialmove3d_sibgrapi.pdf}}
}